
分析 (1)根据对数的定义求出即可;
(2)设:logaM=x,logaN=y,根据对数定义可知:ax=M,ay=N,ax•ay=M•N求出ax+y=M•N,根据对数的定义求出即可;
(3)根据对数的性质对代数式逐步进行化简即可.
解答 解:(1)log21=0,log3$\frac{1}{3}$=-1,
故答案为:0,-1;
(2)①
证明:设:logaM=x,logaN=y,
∵根据对数定义可知:ax=M,ay=N,
∴ax•ay=M•N,
∴ax+y=M•N,
即loga(M•N)=x+y=logaM+logaN;
(3)[(1-log63)2+log62•log618]÷log64
=[log26(log62+log6÷2log62
=(log66+1)÷2
=1.
点评 本题考查了对对数的定义和性质的应用,能根据定义和性质进行变形是解此题的关键,是一道基础题目.


科目:初中数学 来源: 题型:解答题
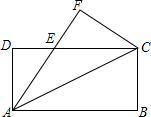 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点F的位置,AF与CD交于点E
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点F的位置,AF与CD交于点E 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
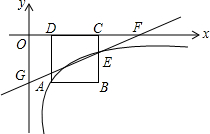 如图,正方形ABCD的顶点C,D在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n,-$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{2}$,0).
如图,正方形ABCD的顶点C,D在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n,-$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{2}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 里程 | 甲类收费(元) | 乙类收费(元) |
| 3千米以下(包含3千米) | 5.00 | 6.00 |
| 3千米以上,每增加1千米 | 1.60 | 1.30 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 可以取任意实数 | B. | 函数图象在第一、三象限 | ||
| C. | 图象过点(1,k)和(-k,-1) | D. | 与函数y=4x的图象有两个交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
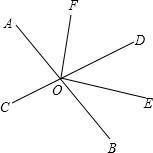 如图,两条直线AB,CD相交于点O,OE平分∠BOD.
如图,两条直线AB,CD相交于点O,OE平分∠BOD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com