
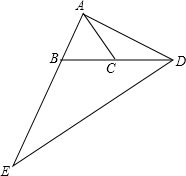
 已知△ABC中,AB=AC,D为BC延长线上一点,且DC=BC,E是AB延长线上的一点,且BE=2AB,求证:DE=2AD.
已知△ABC中,AB=AC,D为BC延长线上一点,且DC=BC,E是AB延长线上的一点,且BE=2AB,求证:DE=2AD. 分析 由AB=AC,推出∠ABC=∠ACB,推出∠EBD=∠ACD,由BE=2AB=2AC,BD=2CD,推出$\frac{BE}{AC}$=$\frac{BD}{CD}$=2,推出△BED∽△CAD,即可解决问题.
解答 证明: ∵AB=AC,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠EBD=∠ACD,
∵BE=2AB=2AC,BD=2CD,
∴$\frac{BE}{AC}$=$\frac{BD}{CD}$=2,
∴△BED∽△CAD,
∴DE:AD=BE:AC=2,
∴ED=2AD.
点评 本题考查相似三角形的判定和性质、等腰三角形的性质等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于中考常考题型.


科目:初中数学 来源:2016-2017学年湖北省武汉市侏儒山街四校八年级3月月考数学试卷(解析版) 题型:单选题
如图,有一块直角三角形纸片,两直角边分别为:AC=6cm, BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
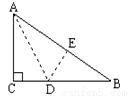
A. 2cm B. 3cm C. 4cm D. 5cm
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
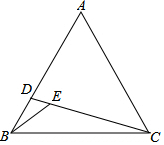 如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,∠BEC=120°,连接BE.若CD=$\frac{14}{3}$,BE=2,△ACD的面积为$\frac{14}{3}$$\sqrt{3}$,则△BCE的面积为2$\sqrt{3}$.
如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,∠BEC=120°,连接BE.若CD=$\frac{14}{3}$,BE=2,△ACD的面积为$\frac{14}{3}$$\sqrt{3}$,则△BCE的面积为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间 | 换表前 | 换表后 | |
| 峰时(8:00-21:00) | 谷时(21:00-8:00) | ||
| 电价 | 每度0.52元 | 每度0.55元 | 每度0.30元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
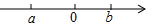 实数a,b在数轴上对应点得位置如图,则化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
实数a,b在数轴上对应点得位置如图,则化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )| A. | 2a-b | B. | b-2a | C. | b | D. | -b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com