
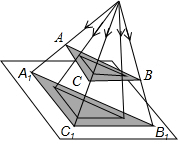
 一块直角三角形板ABC,∠ACB=90°,BC=12cm,AC=8cm,测得BC边的中心投影B1C1长为24cm,则A1B1长为________cm.
一块直角三角形板ABC,∠ACB=90°,BC=12cm,AC=8cm,测得BC边的中心投影B1C1长为24cm,则A1B1长为________cm. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
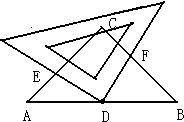 22、如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是AB的中点,将一块直角三角形板的直角顶点放在点D处旋转,两直角边分别交AC于点E,交BC于点F.则图中除了已知的相等的线段外,还有哪些线段相等?请找出来,并对其中一对说明相等的理由.
22、如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是AB的中点,将一块直角三角形板的直角顶点放在点D处旋转,两直角边分别交AC于点E,交BC于点F.则图中除了已知的相等的线段外,还有哪些线段相等?请找出来,并对其中一对说明相等的理由.查看答案和解析>>
科目:初中数学 来源:浙江省杭州市萧山区瓜沥二中2011-2012学年八年级上学期期中质量检测数学试题 题型:044
如图,在RtΔABC中,∠ACB=90°,AC=BC,点D是AB的中点,将一块直角三角形板的直角顶点放在点D处旋转,两直角边分别交AC于点E,交BC于点F.则图中除了已知的相等的线段(AC=BC,AD=BD)外,还有哪些线段相等?请找出来,并对其中一对说明相等的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
操作:在△ABC中,AC=BC=2,∠C=900,将一块等腰三角形板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。图①,②,③是旋转三角板得到的图形中的3种情况。研究:
(1) 三角板绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图②加以证明。
(2) 三角板绕点P旋转,是否能居为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。
(3)若将三角板的直角顶点放在斜边AB上的M处,且AM:MB=1:3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合图④加以证明。

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
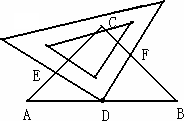
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是AB的中点,将一块直角三角形板的直角顶点放在点D处旋转,两直角边分别交AC于点E,交BC于点F.则图中除了已知的相等的线段外,还有哪些线段相等?请找出来,并对其中一对说明相等的理由.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是AB的中点,将一块直角三角形板的直角顶点放在点D处旋转,两直角边分别交AC于点E,交BC于点F.则图中除了已知的相等的线段外,还有哪些线段相等?请找出来,并对其中一对说明相等的理由.查看答案和解析>>
科目:初中数学 来源: 题型:
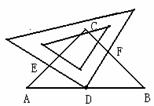
如图,在RtΔABC中, ∠ACB=90O,AC=BC,点D是AB的中点,将一块直角三角形板的直角顶点放在点D处旋转,两直角边分别交AC于点E,交BC于点F.则图中除了已知的相等的线段外,还有哪些线段相等?请找出来,并对其中![]() 一对说明相等的理由.
一对说明相等的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com