
分析 根据x-2y=0(xy≠0),可以对$\frac{y}{{x}^{2}-{y}^{2}}$÷$\frac{1}{x-y}$化简并求得化简后式子的值,本题得以解决.
解答 解:∵x-2y=0(xy≠0),÷
∴x=2y,
∴$\frac{y}{{x}^{2}-{y}^{2}}$÷$\frac{1}{x-y}$
=$\frac{y}{(x+y)(x-y)}×\frac{x-y}{1}$
=$\frac{y}{x+y}$
=$\frac{y}{2y+y}$
=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查分式的化简求值,解题的关键是建立所求式子与已知式子之间的关系.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
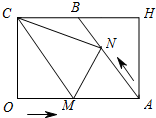 如图,在矩形OAHC中,OC=4,OA=6,B为CH中点,连接AB.动点M从点O出发沿OA边向点A运动;动点N从点A出发沿AB边向点B运动,两个动点同时出发,速度都是每秒1个单位长度,连接CM,CN,MN,设运动时间为t(秒)(0<t<5).解答下列问题:
如图,在矩形OAHC中,OC=4,OA=6,B为CH中点,连接AB.动点M从点O出发沿OA边向点A运动;动点N从点A出发沿AB边向点B运动,两个动点同时出发,速度都是每秒1个单位长度,连接CM,CN,MN,设运动时间为t(秒)(0<t<5).解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下列材料:
阅读下列材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
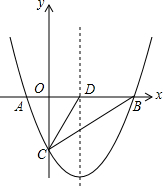 如图,抛物线y=$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1,0),C(0,-2).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1,0),C(0,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com