
如图①,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
1.试猜想线段BG和AE的数量关系,请直接写出你得到的结论.
2.将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图②,通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.
3.若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,求AF的值.


见解析
解析:解:(1)BG=AE.
(2)成立.
如图②,连接AD.
∵△ABC是等腰三直角角形,∠BAC=90°,点D是BC的中点.
∴∠ADB=90°,且BD=AD.
∵∠BDG=∠ADB-∠ADG=90°-∠ADG=∠ADE,DG=DE.
∴△BDG≌△ADE,∴BG=AE.
(3)由(2)知,BG=AE,故当BG最大时,AE也最大.
因为正方形DEFG在绕点D旋转的过程中,G点运动的图形是以点D为圆心,DG为半径的圆,故当正方形DEFG旋转到G点位于BC的延长线上(即正方形DEFG绕点D逆时针方向旋转270°)时,BG最大,如图③.
若BC=DE=2,则AD=1,EF=2.
在Rt△AEF中,AF 2=AE 2+EF 2=(AD+DE)2+EF 2=(1+2)2+2 2=13.
∴AF=![]() .
.
即在正方形DEFG旋转过程中,当AE为最大值时,AF=![]() .
.

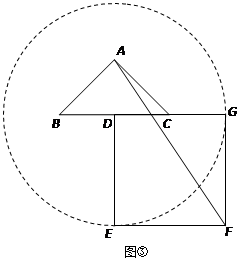


科目:初中数学 来源: 题型:
 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.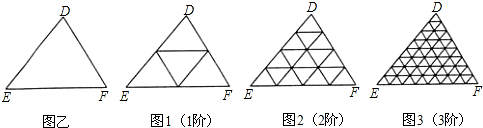
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=
如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com