
【题目】已知I是△ABC的内心,AI延长线交△ABC外接圆于D,连BD.
(1)在图1中,求证:DB=DI;
(2)如图2,若AB为直径,且OI⊥AD于I点,DE切圆于D点,求sin∠ADE的值.
【答案】
(1)解:连接BI,

∵I是△ABC的内心,
∴AD平分∠CAB,BI平分∠ABC,
∴∠CAD=∠BAD,∠ABI=∠CBI,
∵∠CAD=∠DBC,
∴∠DAB=∠CBD,
∵∠DBI=∠DBC+∠CBI,
∠DIB=∠DAB+∠IBA,
∴∠DIB=∠DBI,
∴BD=DI;
(2)解:连接BD,

∵AB为直径,
∴∠ADB=90°,
∵OI⊥AD,
∴AD=2DI,
∵BD=DI,
∴AD=2BD,
∴AB= ![]() =
= ![]() BD,
BD,
∵DE切圆于D点,
∴∠ABD=∠ADE,
∴sin∠ADE=sin∠ABD= ![]() =
= ![]() .
.
【解析】(1)连接BI,依据三角形的内心的定义可得到AD平分∠CAB,BI平分∠ABC,根据角平分线的定义得到∠CAD=∠BAD,∠ABI=∠CBI,得到结合圆周角定理可得到∠DAB=∠CBD,然后再依据三角形的外角的性质得到∠DIB=∠DBI,最后,依据等角对等边的性质可得到BD=DI;
(2)连接BD,根据圆周角定理的推理可得到∠ADB=90°,然后再依据垂径定理得到AD=2DI,接下来,利用勾股定理求得AB的长,,根据弦切角定理得到∠ABD=∠ADE,接下来,依据锐角三角函数的定义求解即可.
【考点精析】利用圆周角定理对题目进行判断即可得到答案,需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为线段
为线段![]() 上一点,一副直角三角板的直角顶点与点
上一点,一副直角三角板的直角顶点与点![]() 重合,直角边
重合,直角边![]() 、
、![]() 在线段
在线段![]() 上,
上,![]() .
.

(1)将图1中的三角板![]() 绕着点
绕着点![]() 沿顺时针方向旋转到如图2所示的位置,若
沿顺时针方向旋转到如图2所示的位置,若![]() ,则
,则![]() ________;猜想
________;猜想![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(2)将图1中的三角板![]() 绕着点
绕着点![]() 沿逆时针方向按每秒
沿逆时针方向按每秒![]() 的速度旋转一周,三角板
的速度旋转一周,三角板![]() 不动,请问几秒时
不动,请问几秒时![]() 所在的直线平分
所在的直线平分![]() ?
?
(3)将图1中的三角板![]() 绕着点
绕着点![]() 沿逆时针方向按每秒
沿逆时针方向按每秒![]() 的速度旋转一周,同时三角板
的速度旋转一周,同时三角板![]() 绕着点
绕着点![]() 沿顺时针方向按每秒
沿顺时针方向按每秒![]() 的速度旋转(随三角板
的速度旋转(随三角板![]() 停止而停止),请计算几秒时
停止而停止),请计算几秒时![]() 与
与![]() 的角分线共线.
的角分线共线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
(1)求证:AP是⊙O的切线;
(2)求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD.
(1)如图1,请直接写出∠BME、∠E、∠END的数量关系为 ;
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
(3)如图3,∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,直线MB、ND交于点F,则
∠NDE,直线MB、ND交于点F,则![]() =___.
=___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).
(1)补全坐标系并指出△ABC和△A'B'C'满足什么几何变换(直接写答案)?
(2)作△A'B'C'关于x轴对称图形△A''B''C'';
(3)△ABC和△A''B''C''满足什么几何变换?求A''、B''、C''三点坐标(直接写答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC向右平移3个单位长度,再向上平移2个单位长度,可以得到![]() .
.

(1)画出平移后的![]() ;
;
(2)写出![]() 三个顶点的坐标;
三个顶点的坐标;
(3)已知点P在x轴上,以![]() 、
、![]() 、P为顶点的三角形面积为4,求点P的坐标.
、P为顶点的三角形面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③当x=4时,甲、乙两队所挖管道长度相同;
④甲队比乙队提前2天完成任务.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于A,B与y轴交于C,过C作x轴的平行线交抛物线于点D,过点D作x轴的垂线交x轴于E,点D的坐标为(2,3)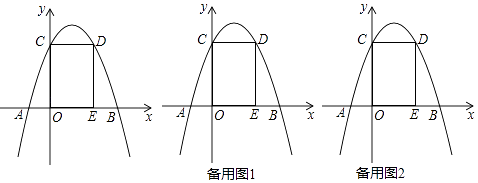
(1)求抛物线的解析式;
(2)点P为第一象限直线DE右侧抛物线上一点,连接AP交y轴于点F,连接PD、DF,设点P的横坐标为t,△PFD的面积为S,求S与t的函数关系式;
(3)在(2)的条件下,点P向下平移3个单位得到点Q,连接AQ、EQ,若∠AQE=45°,求点P的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com