

���� ��1���ٸ��ݡ�C�ġ������㡱�Ķ��弴���жϣ�
������P�ڵ�һ�����ڣ���PQ��x���ڵ�Q����ͼ1�У��ɵ�P��ֱ��y=$\sqrt{3}$x�ϣ�OP=1���ɵ�OQ=$\frac{1}{2}$��PQ=$\frac{\sqrt{3}}{2}$���Ƴ�P��$\frac{1}{2}$��$\frac{\sqrt{3}}{2}$�����ٸ��ݶԳ��Կɵ���һ���������㡱��
��2�����ڡ�C������һ���������㡱P����|PA-PB|=2���Ƴ�|CP+2-��2-CP��|=2���ɵ�CP=1���Ƴ���������ĵ�P������CP=1������|CP+2-��2-CP��|=2���Ƴ�����|PA-PB|=2���ʴ�ʱ��PΪ��C�ġ������㡱����ˣ���C�ġ������㡱���Ե�CΪԲ�ģ�1Ϊ�뾶��Բ����ͼ2�У���ֱ��y=$\sqrt{3}$x+1��y�ύ�ڵ�D������C�ƶ�����y���������е��ڵ�D���·�ʱ��t��ֵ��С�����е�ΪE������CE���ɡ�DOF�ס�DEC���ɵ�$\frac{OD}{DE}$=$\frac{OF}{CE}$���Ƴ�DE=$\sqrt{3}$��t����СֵΪ1-$\sqrt{3}$�����ٸ��ݶԳ��Կɵ�t�����ֵ���ɴ˼��ɽ�����⣻
��� �⣺��1����M���ǡ�O�ġ������㡱��
��N�ǡ�O�ġ������㡱��
��T�ǡ�O�ġ������㡱��
�ʴ�Ϊ���ǣ��ǣ��ǣ�
�ڸ������⣬|PA-PB|=2��
��|OP+2-��2-OP��|=2��
��OP=1��
����P�ڵ�һ�����ڣ���PQ��x���ڵ�Q����ͼ1�У�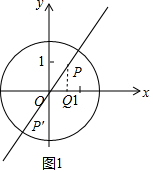
�ߵ�P��ֱ��y=$\sqrt{3}$x�ϣ�OP=1��
��OQ=$\frac{1}{2}$��PQ=$\frac{\sqrt{3}}{2}$��
��P��$\frac{1}{2}$��$\frac{\sqrt{3}}{2}$����
����P�ڵ��������ڣ����ݶԳ��Կ�֪������Ϊ��-$\frac{1}{2}$��-$\frac{\sqrt{3}}{2}$����
����������PO�ij�Ϊ1����P������Ϊ��$\frac{1}{2}$��$\frac{\sqrt{3}}{2}$����-$\frac{1}{2}$��-$\frac{1}{2}$����
��2�����ڡ�C������һ���������㡱P����|PA-PB|=2��
��|CP+2-��2-CP��|=2��
��CP=1��
���������ĵ�P������CP=1������|CP+2-��2-CP��|=2��
��|PA-PB|=2���ʴ�ʱ��PΪ��C�ġ������㡱����ˣ���C�ġ������㡱���Ե�CΪԲ�ģ�1Ϊ�뾶��Բ��
��ͼ2�У���ֱ��y=$\sqrt{3}$x+1��y�ύ�ڵ�D������C�ƶ�����y���������е��ڵ�D���·�ʱ��t��ֵ��С��
���е�ΪE������CE��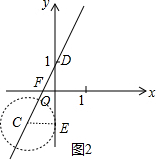
�ߡ�C��Բ����ֱ��y=$\sqrt{3}$x+1�ϣ�
���ֱ�ߺ�x�ᣬy��Ľ���C��0��1����F��-$\frac{\sqrt{3}}{3}$��0����
��OF=$\frac{\sqrt{3}}{3}$��OD=1��
��CE��OF��
���DOF�ס�DEC��
��$\frac{OD}{DE}$=$\frac{OF}{CE}$��
��$\frac{1}{DE}$=$\frac{\frac{\sqrt{3}}{3}}{2}$��
��DE=$\sqrt{3}$��t����СֵΪ1-$\sqrt{3}$��
����C�ƶ�����y���������е��ڵ�D���Ϸ�ʱ��t��ֵ���
ͬ���ɵ�t�����ֵΪ1+$\sqrt{3}$��
����������t��ȡֵ��ΧΪ1-$\sqrt{3}$��t��1+$\sqrt{3}$��
���� ���⿼��Բ�ۺ��⡢һ�κ�����Ӧ�á���ֱ�������Ρ����ߵ����ʡ����������ε��ж������ʵ�֪ʶ������Ĺؼ������Ӧ����ѧ֪ʶ������⣬ѧ���� ���̵�˼��˼�����⣬�����п�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
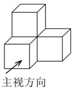 ��ͼ�����ĸ���ͬ��С��������ɵ�����ͼ�Σ���������ͼ�ǣ�������
��ͼ�����ĸ���ͬ��С��������ɵ�����ͼ�Σ���������ͼ�ǣ�������| A�� |  | B�� | 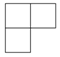 | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
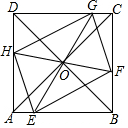 ��ͼ��������ABCD�ı߳�Ϊ1��E��F��G��H�ֱ���AB��BC��CD��DA���ϵĶ��㣨�����˵㣩����EG��FH���������ε�����O��
��ͼ��������ABCD�ı߳�Ϊ1��E��F��G��H�ֱ���AB��BC��CD��DA���ϵĶ��㣨�����˵㣩����EG��FH���������ε�����O���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
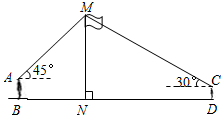 ��ͼ��ij��ѧ��ȤС���ڻ���ϲ���ѧУ��˸߶ȣ���֪С�����۾������ľ���AB=1.7m������˶���M������Ϊ45�㣻С����۾������ľ���CD=1.5m������˶���M������Ϊ30�㣮�������28����λ��������ࣨ��B��N��D��ͬһ��ֱ���ϣ�����������MN�ĸ߶ȣ����ο����ݣ�$\sqrt{2}$��1.4��$\sqrt{3}$��1.7���������������
��ͼ��ij��ѧ��ȤС���ڻ���ϲ���ѧУ��˸߶ȣ���֪С�����۾������ľ���AB=1.7m������˶���M������Ϊ45�㣻С����۾������ľ���CD=1.5m������˶���M������Ϊ30�㣮�������28����λ��������ࣨ��B��N��D��ͬһ��ֱ���ϣ�����������MN�ĸ߶ȣ����ο����ݣ�$\sqrt{2}$��1.4��$\sqrt{3}$��1.7����������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com