
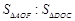 = .
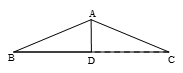
= .
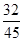 .
.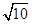 x,由三角形的面积公式求出DG的值,由三角函数值求出AG,就可以表示出AE,从而求出AF,再由△AFO∽△DCO就可以求出结论.解答:解:作DG⊥AB于G,DH⊥AC与H,
x,由三角形的面积公式求出DG的值,由三角函数值求出AG,就可以表示出AE,从而求出AF,再由△AFO∽△DCO就可以求出结论.解答:解:作DG⊥AB于G,DH⊥AC与H,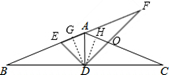
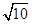 x,
x,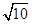 x.
x.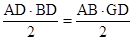 ,
, ,
,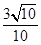 .
.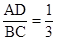 =tan∠C.
=tan∠C.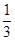 .
.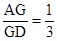 ,
,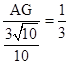 ,
,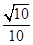 x.
x.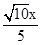 .
.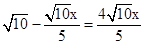 .
.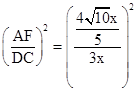 =
=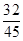 .
.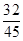 .
.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
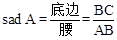 . 我们容易知道一个角的大小与这个角的正对值也是互相唯一确定的.根据上述角的正对定义,解下列问题:
. 我们容易知道一个角的大小与这个角的正对值也是互相唯一确定的.根据上述角的正对定义,解下列问题: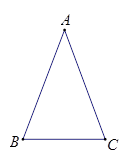
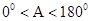 ,
,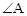 的正对值sadA的取值范围是_____________。
的正对值sadA的取值范围是_____________。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com