
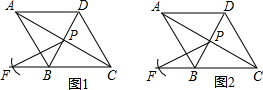
 如图1和如图2,四边形ABCD是菱形,P是对角线BD上一点,以点P为圆心,PC为半径画弧,交CB(或延长线)于点F,连结PF,PA,PC.
如图1和如图2,四边形ABCD是菱形,P是对角线BD上一点,以点P为圆心,PC为半径画弧,交CB(或延长线)于点F,连结PF,PA,PC.科目:初中数学 来源: 题型:
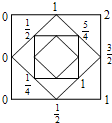 如图,在一个正方形的四个顶点处,按逆时针方向各写一个数:2,0,0,1,然后取各边的中点,并在各中点处写上其所在边两端点处的两个数的平均值.这四个中点构成一个新的正方形,又在这个新的正方形四边中点处写上其所在边两个端点处的两个数的平均值.连续这样做到第十个正方形,则图上写出的所有数的和
如图,在一个正方形的四个顶点处,按逆时针方向各写一个数:2,0,0,1,然后取各边的中点,并在各中点处写上其所在边两端点处的两个数的平均值.这四个中点构成一个新的正方形,又在这个新的正方形四边中点处写上其所在边两个端点处的两个数的平均值.连续这样做到第十个正方形,则图上写出的所有数的和查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第3章《圆》中考题集(50):3.5 直线和圆的位置关系(解析版) 题型:解答题
 ,点M是AD的中点,P是线段MD上的一动点(P不与M,D重合),以AB为直径作⊙O,过点P作⊙O的切线交BC于点F,切点为E.
,点M是AD的中点,P是线段MD上的一动点(P不与M,D重合),以AB为直径作⊙O,过点P作⊙O的切线交BC于点F,切点为E.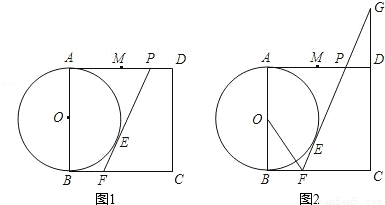
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com