
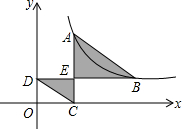
 如图,点A,B在反比例函数y=$\frac{k}{x}$(x>0)的图象中,AC⊥x轴于点C,BD⊥y轴于点D,交AC于点F,连接AB,CD,若图中的阴影部分的面积和为5,且AE=2CE,则k的值为( )
如图,点A,B在反比例函数y=$\frac{k}{x}$(x>0)的图象中,AC⊥x轴于点C,BD⊥y轴于点D,交AC于点F,连接AB,CD,若图中的阴影部分的面积和为5,且AE=2CE,则k的值为( )| A. | 5 | B. | 6 | C. | 10 | D. | 12 |
分析 根据反比例函数图象上点的坐标特征,设A(t,$\frac{k}{t}$),则AE=$\frac{2k}{3t}$,CE=$\frac{t}{3}$=$\frac{k}{3t}$,于是可表示出B(3t,$\frac{k}{3t}$),然后根据三角形面积公式得到$\frac{1}{2}$•t•$\frac{k}{3t}$+$\frac{1}{2}$•$\frac{2K}{3t}$•2t=5,再解关于k的方程即可.
解答 解:设A(t,$\frac{k}{t}$),
∵AC⊥x轴于点C,BD⊥y轴于点D,AE=2CE,
∴AE=$\frac{2k}{3t}$,CE=$\frac{t}{3}$=$\frac{k}{3t}$,
∴B(3t,$\frac{k}{3t}$),
∵图中的阴影部分的面积和为5,
∴$\frac{1}{2}$•t•$\frac{k}{3t}$+$\frac{1}{2}$•$\frac{2K}{3t}$•2t=5,
∴k=6.
故选B.
点评 本题考查了反比例函数系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.


科目:初中数学 来源: 题型:解答题
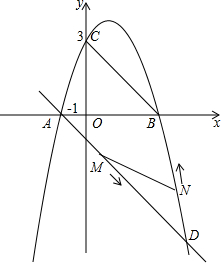 如图,二次函数y=ax2+2x+c的图象与x轴交于点A(-1,0)和点B,与y轴交于点C(0,3).
如图,二次函数y=ax2+2x+c的图象与x轴交于点A(-1,0)和点B,与y轴交于点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).
已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
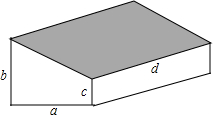 如图,要修建一个蔬菜大棚,棚的横截面是直角梯形,棚宽a=6米,棚高分别为b=5米,c=2米,长为d=30米,现要在棚顶覆盖塑料膜(即图中阴影部分),求共计需要塑料膜多少平方米?
如图,要修建一个蔬菜大棚,棚的横截面是直角梯形,棚宽a=6米,棚高分别为b=5米,c=2米,长为d=30米,现要在棚顶覆盖塑料膜(即图中阴影部分),求共计需要塑料膜多少平方米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
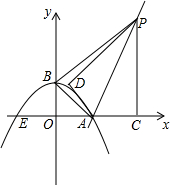 已知:如图,抛物线y=ax2+bx+c与x轴交于点A(4,0)、E(-2,0)两点,与y轴交于点B(0,2,),连结AB.过点A作直线AK⊥AB,动点P从点A出发以每秒$\sqrt{5}$个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.
已知:如图,抛物线y=ax2+bx+c与x轴交于点A(4,0)、E(-2,0)两点,与y轴交于点B(0,2,),连结AB.过点A作直线AK⊥AB,动点P从点A出发以每秒$\sqrt{5}$个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
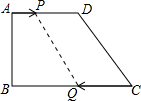 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com