

分析 (1)问题探究:根据AE=BF=CG=DH=1,∠AFO=∠BGM=∠CHN=∠DEP=45°,可得△AER,△BFS,△CGT,△DHW是四个全等的等腰直角三角形,进而得出AD=WE=a;根据所得的四个等腰直角三角形的斜边长为a,可得新正方形与原正方形ABCD的面积相等;根据图形可得4×(S△FSB+S四边形MFBG)=S正方形MNPQ+4×S四边形MFBG,即S正方形MNPQ=4S△FSB;
(2)问题解决:根据S△FSB=$\frac{1}{2}$×1×1=$\frac{1}{2}$,即可求得S正方形MNPQ=4S△FSB=4×$\frac{1}{2}$=2;
(3)拓展应用:根据图形,△PDH,△QWEI,△RFG是三个全等的三角形,可以拼成一个和△ABC一样的等边三角形(无缝隙,不重叠),进而得出S△PRQ=S△ADG+S△BHE+S△CFI=3S△ADG,再过点G作GJ⊥BA于J,根据GJ=$\frac{\sqrt{3}}{2}$AG=$\frac{\sqrt{3}}{2}$,可得S△ADG,最后根据S△PQR=3S△ADG进行计算即可.
解答 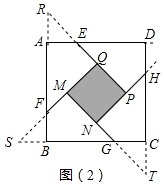 解:(1)问题探究:
解:(1)问题探究:
∵AE=BF=CG=DH=1,∠AFO=∠BGM=∠CHN=∠DEP=45°,
∴△AER,△BFS,△CGT,△DHW是四个全等的等腰直角三角形,
∴AE=DW,
∴AE+DE=DW+DE=a,即AD=WE=a,
∵拼成一个新的正方形无缝隙,不重叠,
∴这个新正方形的边长为a;
∵所得的四个等腰直角三角形的斜边长为a,则斜边上的高为$\frac{1}{2}$a,
每个等腰直角三角形的面积为:$\frac{1}{2}$a•$\frac{1}{2}$a=$\frac{1}{4}$a2,
∴拼成的新正方形面积为:4×$\frac{1}{4}$a2=a2,
即新正方形与原正方形ABCD的面积相等;
∵新正方形的面积=4×S△MSG=4×(S△FSB+S四边形MFBG),
原正方形ABCD的面积=S正方形MNPQ+4×S四边形MFBG,
∴4×(S△FSB+S四边形MFBG)=S正方形MNPQ+4×S四边形MFBG,
即S正方形MNPQ=4S△FSB;
故答案为:a,=,S正方形MNPQ=4S△FSB;
(2)问题解决:
∵S△FSB=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
∴S正方形MNPQ=4S△FSB=4×$\frac{1}{2}$=2;
(3)拓展应用: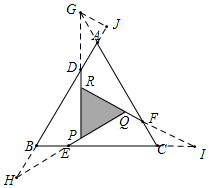
如图所示,△PDH,△QWEI,△RFG是三个全等的三角形,可以拼成一个和△ABC一样的等边三角形(无缝隙,不重叠),
∴S△PRQ=S△ADG+S△BHE+S△CFI=3S△ADG,
如图,过点G作GJ⊥BA于J,
根据∠ADG=∠BDP=30°,∠DAF=60°=∠GAJ可得,∠ADG=∠AGD=30°,
∴AD=AG=1,
∴GJ=$\frac{\sqrt{3}}{2}$AG=$\frac{\sqrt{3}}{2}$,
∴S△ADG=$\frac{1}{2}$AD×GJ=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$,
∴S△PQR=3S△ADG=3×$\frac{\sqrt{3}}{4}$=$\frac{3}{4}\sqrt{3}$.
点评 本题属于四边形综合题,主要考查了正方形的性质,等腰直角三角形的性质,等边三角形的性质以及全等三角形的性质的综合应用,解决问题的关键是作作辅助线构造直角三角形进行求解.通过本题我们可以体会到,运用等积变换的数学思想,不仅简化了几何计算,而且形象直观,易于理解,体现了数学的魅力.


科目:初中数学 来源: 题型:解答题
 如图,AD为△ABC的中线,AB=AC,∠BAC=45°,过点C作CE⊥AB,垂足为E,CE与AD交于点F.
如图,AD为△ABC的中线,AB=AC,∠BAC=45°,过点C作CE⊥AB,垂足为E,CE与AD交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月工资/元 | 9000 | 6500 | 4000 | 3600 | 3000 | 1500 |
| 人数/人 | 1 | 1 | 4 | 3 | 2 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=1,OC=6,试求出正方形ADEF的边长.
如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=1,OC=6,试求出正方形ADEF的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 列方程解应用题:
列方程解应用题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com