
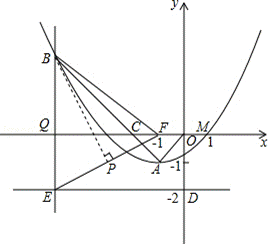
如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(﹣1,﹣1),与x轴交点M(1,0).C为x轴上一点,且∠CAO=90°,线段AC的延长线交抛物线于B点,另有点F(﹣1,0).
(1)求抛物线的解析式;
(2)求直线Ac的解析式及B点坐标;
(3)过点B做x轴的垂线,交x轴于Q点,交过点D(0,﹣2)且垂直于y轴的直线于E点,若P是△BEF的边EF上的任意一点,是否存在BP⊥EF?若存在,求P点的坐标,若不存在,请说明理由.
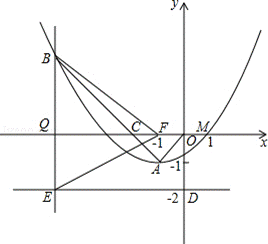
解:(1)设抛物线解析式为:y=a(x+1)2﹣1,将(1,0)代入得:
0=a(1+1)2﹣1,
解得;a=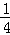 ,
,
∴抛物线的解析式为:y=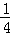 (x+1)2﹣1;
(x+1)2﹣1;
(2)∵A(﹣1,﹣1),
∴∠COA=45°,
∵∠CAO=90°,
∴△CAO是等腰直角三角形,
∴AC=AO,
∴C(﹣2,0),
设直线AC的解析式为:y=kx+b,
将A,C点代入得出: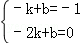 ,
,
解得: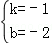 ,
,
∴直线AC的解析式为:y=﹣x﹣2,
将y=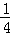 (x+1)2﹣1和y=﹣x﹣2联立得:
(x+1)2﹣1和y=﹣x﹣2联立得:
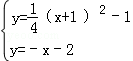 ,
,
解得: ,
,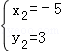 ,
,
∴直线AC的解析式为:y=﹣x﹣2,B点坐标为:(﹣5,3);
(3)过点B作BP⊥EF于点P,
由题意可得出:E(﹣5,﹣2),设直线EF的解析式为:y=dx+c,
则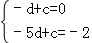 ,
,
解得: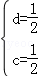 ,
,
∴直线EF的解析式为:y= x+
x+ ,
,
∵直线BP⊥EF,∴设直线BP的解析式为:y=﹣2x+e,
将B(﹣5,3)代入得出:3=﹣2×(﹣5)+e,
解得:e=﹣7,
∴直线BP的解析式为:y=﹣2x﹣7,
∴将y=﹣2x﹣7和y=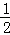 x+
x+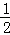 联立得:
联立得:
 ,
,
解得: ,
,
∴P(﹣3,﹣1),
故存在P点使得BP⊥EF,此时P(﹣3,﹣1).


科目:初中数学 来源: 题型:
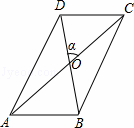
如图,在▱ABCD中,对角线AC、BD相交成的锐角为α,若AC=a,BD=b,则▱ABCD的面积是( )
|
| A. |
| B. | absinα | C. | abcosα | D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
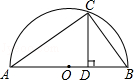
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB交AB于D.已知cos∠ACD=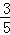 ,BC=4,则AC的长为( )
,BC=4,则AC的长为( )
|
| A. | 1 | B. |
| C. | 3 | D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2 .
.
以上结论中,你认为正确的有( )个.

|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
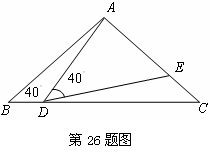
如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段AB上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线AC段于E.
(1)当∠BDA=115°时,∠BAD= °, ∠DEC= °点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);;
(2)当DC等于多少时,△ABD与△DCE全等?请说明理由;
(3) 在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com