
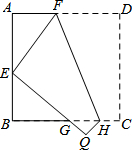
 如图,将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,则△FAE与△EBG的面积之比为( )
如图,将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,则△FAE与△EBG的面积之比为( )| A. | 4:9 | B. | 2:3 | C. | 3:4 | D. | 9:16 |
分析 设AB=BC=CD=AD=16,于是得到AE=EB=8,EF=FD,设EF=DF=x.则AF=16x,根据勾股定理得到AF=16-10=6,根据折叠的性质得到∠FEG=90°,根据相似三角形的性质即可得到结论.
解答 解:∵四边形ABCD是正方形,
∴设AB=BC=CD=AD=16,
∵AE=EB=8,EF=FD,设EF=DF=x.则AF=16-x,
在RT△AEF中,∵AE2+AF2=EF2,
∴82+(16-x)2=x2,
∴x=10,
∴AF=16-10=6,
∵∠A=∠B=∠D=90°,
∵将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,
∴∠FEG=90°,
∴∠AEF+∠BEG=∠AEF+∠AFE=90°,
∴∠AFE=∠BEG,
∴△AFE∽△BEG,
∴$\frac{{S}_{△AEF}}{{S}_{△BGE}}$=($\frac{AF}{BE}$)2=$\frac{9}{16}$,
故选D.
点评 本题考查翻折变换、正方形的性质、勾股定理等知识,相似三角形的判定和性质,解题的关键是设未知数利用勾股定理列出方程解决问题,属于中考常考题型.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | $-\frac{2}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 9 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.6×1012 | B. | 1.6×1010 | C. | 1.6×104 | D. | 1.6×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com