
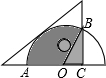
 将一块三角板和半圆形量角器按图中方式叠放,重叠部分(阴影)的量角器的圆弧AB对应的圆心角∠AOB=120°,OC=2cm,则图中阴影部分的面积为($\frac{16π}{3}$+2$\sqrt{3}$)cm2.
将一块三角板和半圆形量角器按图中方式叠放,重叠部分(阴影)的量角器的圆弧AB对应的圆心角∠AOB=120°,OC=2cm,则图中阴影部分的面积为($\frac{16π}{3}$+2$\sqrt{3}$)cm2. 分析 根据题意可以求得∠BOC和∠OBC的度数,然后根据直角三角形的知识可以求得OB和BC的长,然后根据扇形的面积公式和直角三角形的面积公式可以求得阴影部分的面积.
解答 解:∵∠AOB=120°,OC=2cm,∠BCO=90°,
∴∠BOC=180°-∠AOB=60°,
∴∠OBC=30°,
∴OB=4,BC=2$\sqrt{3}$,
∴图中阴影部分的面积为:$\frac{120×π×{4}^{2}}{360}+\frac{2×2\sqrt{3}}{2}$=$\frac{16π}{3}+2\sqrt{3}$,
故答案为:($\frac{16π}{3}$+2$\sqrt{3}$)cm2;
点评 本题考查扇形面积的计算,解答本题的关键是明确题意,找出所求问题需要的条件,利用扇形的面积公式和直角三角形的知识解答.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
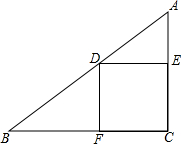 如图所示,D是Rt△ABC斜边上的一点,DE⊥AC,DF⊥BC,垂足分别为E,F,且DE=DF.若AD=3,DB=4,试求S△ADE+S△BDF的值.
如图所示,D是Rt△ABC斜边上的一点,DE⊥AC,DF⊥BC,垂足分别为E,F,且DE=DF.若AD=3,DB=4,试求S△ADE+S△BDF的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=x2=0 | B. | x1=2$\sqrt{3}$,x2=-2$\sqrt{3}$ | C. | x1=2,x2=-2 | D. | x1=4,x2=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
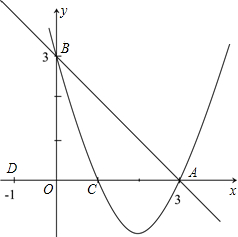 如图,已知C点的坐标为(1,0),直线y=-x+3交于x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A,B,C三点.
如图,已知C点的坐标为(1,0),直线y=-x+3交于x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A,B,C三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
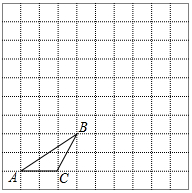 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com