
 于点P1,此时直线l的函数表达式是y=2x+1.
于点P1,此时直线l的函数表达式是y=2x+1.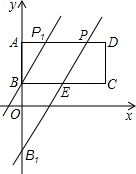
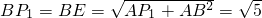 ,
,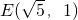 ,
,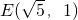 代入得
代入得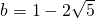 ,
,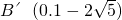 ,
,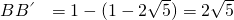 ;
; S矩形ABCD或S梯形ABEP=
S矩形ABCD或S梯形ABEP= S矩形ABCD,
S矩形ABCD,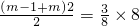 或
或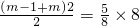 .
.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
 若一个矩形的短边与长边的比值为
若一个矩形的短边与长边的比值为
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
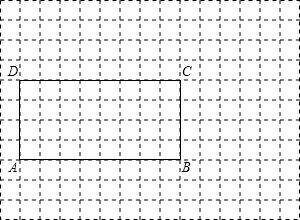
 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=| 3 |
A、3
| ||
| B、3 | ||
C、4
| ||
| D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
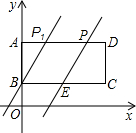 于点P1,此时直线l的函数表达式是y=2x+1.
于点P1,此时直线l的函数表达式是y=2x+1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com