

���� ��1�����ݾ���ֵ�Լ�ż�η��ķǸ��Լ������a��b��ֵ��
��2����C���Ӧ��������Ϊx�����ݡ�����һ�뵽��AC���е㣬�־�������֮��BC���е㡱�������г�����x��һԪһ�η��̣��ⷽ�̼��ɵó����ۣ�
��3�����ݵ�P���˶�����ͬ��0��t��3��3��t��6��9��t�����ǣ�����PB=2QB�г�����t��һԪһ�η��̣��ⷽ�̼��ɵó����ۣ�
��� �⣺��1����$\frac{1}{2}$��a-12��2+|b+6|=0��
��a=12��b=-6��
��2����C���Ӧ��������Ϊx��
���������֪��12-$\frac{x-6}{2}$=4����12-$\frac{x+12}{2}$����
��ã�x=6��
���C����Ӧ��������Ϊ6��
��3������P�˶�����Aʱ����2t=12-6��
��ã�t=3��
�ٵ�0��t��3ʱ����P��Ӧ��������Ϊ6+2t����Q��Ӧ��������Ϊ6-4t��
��PB=2QB��
��6+2t-��-6��=2��|6-4t-��-6��|��
��ã�t1=$\frac{6}{5}$��t2=6����ȥ����
�ڵ�3��t��6ʱ����P��Ӧ��������Ϊ12-2��t-3������Q��Ӧ��������Ϊ6-4t��
��PB=2QB��
��12-2��t-3��-��-6��=2��[-6-��6-4t��]��
��ã�t3=$\frac{24}{5}$��
�۵�9��tʱ��������PB=2QB��
���Ͽ�֪����tΪ$\frac{6}{5}$���$\frac{24}{5}$��ʱPB=2QB��
���� ���⿼���˾���ֵ�Լ�ż�η��ķǸ��ԡ������Լ�һԪһ�η��̵�Ӧ�ã�����������ϵ�г�һԪһ�η����ǽ���Ĺؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
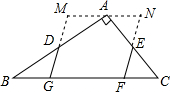 ��ͼ����Rt��ABC�У���BAC=90�㣬AB=4��AC=3����D��E�ֱ���AB��AC���е㣬��G��F��BC���ϣ�������˵��غϣ���DG��EF������BDG�Ƶ�D˳ʱ����ת180�㣬����CEF�Ƶ�E��ʱ����ת180�㣬ƴ���ı���MGFN�����ı���MGFN�ܳ�l��ȡֵ��Χ��$\frac{49}{5}$��l��13����
��ͼ����Rt��ABC�У���BAC=90�㣬AB=4��AC=3����D��E�ֱ���AB��AC���е㣬��G��F��BC���ϣ�������˵��غϣ���DG��EF������BDG�Ƶ�D˳ʱ����ת180�㣬����CEF�Ƶ�E��ʱ����ת180�㣬ƴ���ı���MGFN�����ı���MGFN�ܳ�l��ȡֵ��Χ��$\frac{49}{5}$��l��13�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | �� | -4 | -3 | -2 | -1 | 0 | �� |
| y=-��x+2��2+1 | �� | �� | 0 | 1 | 0 | -3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com