
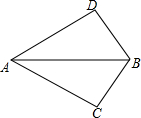
 如图所示,已知∠ABD=∠ABC,补充一个条件,可使△ABD≌△ABC,那么补充的条件不能是( )
如图所示,已知∠ABD=∠ABC,补充一个条件,可使△ABD≌△ABC,那么补充的条件不能是( )| A. | AD=AC | B. | BD=CB | C. | ∠D=∠C | D. | ∠DAB=∠CAB |
分析 全等三角形的判定定理有SAS,ASA,AAS,SSS,已知有∠DAB=∠CAB和隐含条件AB=AB,看看再添加的条件和以上两个条件是否符合全等三角形的判定定理即可.
解答 解:A、AD=AC,AB=AB,∠ABD=∠ABC,
∴SSA不能推出△ABC≌△ABD,故本选项符合题意;
B、∵BD=CB,∠ABD=∠ABC,AB=AB,
∴根据SAS能推出△ABC≌△ABD,故本选项不符合题意;
C、∵∠D=∠C,∠ABD=∠ABC,AB=AB,
∴根据AAS能推出△ABC≌△ABD,故本选项不符合题意;
D、∵∠DAB=∠CAB,AB=AB,∠ABD=∠ABC,
根据ASA能推出△ABC≌△ABD,故本选项不符合题意;
故选A.
点评 本题考查了全等三角形判定定理的应用,注意:全等三角形的判定定理有:SAS,ASA,AAS,SSS.


科目:初中数学 来源: 题型:解答题
 如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条平行线倍第三条直线所截,一对内错角的角平分线互相平行 | |
| B. | 同角的余角相等 | |
| C. | 在同一平面内,不相交的两条线段必平行 | |
| D. | 在同一平面内,若a⊥b,b⊥c,则a∥c |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1<x3<x2 | B. | x<1x2<x3 | C. | x3<x2<x1 | D. | x2<x3<x1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 成中心对称的两个图形全等 | |
| B. | 成中心对称的两个图形中,对称点的连线被对称轴平分 | |
| C. | 中心对称图形的对称中心是对称点连线的中心 | |
| D. | 中心对称图形绕对称中心旋转180°后,都能与自身重合 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com