
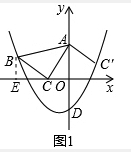
 在△ABC中,∠ACB=90°,点A的坐标为(0,2),点B(-3,1)在抛物线y=ax2+ax-2上,点C在x轴上.
在△ABC中,∠ACB=90°,点A的坐标为(0,2),点B(-3,1)在抛物线y=ax2+ax-2上,点C在x轴上. ;
;
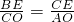 ,
,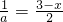 ,
,
 ,CC′=
,CC′= ,∠CAC′=90°,
,∠CAC′=90°, x2+
x2+ x-2得:
x-2得: ×1+
×1+ ×1-2=-1,
×1-2=-1, x2+
x2+ x-2=
x-2= (x+
(x+ )2-
)2-
 ,-
,- ),
), ≈4.42,DM+MB=
≈4.42,DM+MB=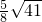 +
+
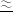 4.517,
4.517, ,CC′=
,CC′= ,∠CAC′=90°,进而求出B′的坐标,代入函数的解析式验证即可;②由抛物线的解析式可求出顶点M坐标(-
,∠CAC′=90°,进而求出B′的坐标,代入函数的解析式验证即可;②由抛物线的解析式可求出顶点M坐标(- ,-
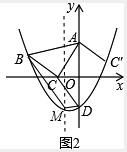
,- ),物线与y轴的交点为D、P、Q两点同时从D点出发,点P沿折线D→C→B运动到点B,点Q沿抛物线(在第二、三象限的部分)运动到点B,则DC+BC=2
),物线与y轴的交点为D、P、Q两点同时从D点出发,点P沿折线D→C→B运动到点B,点Q沿抛物线(在第二、三象限的部分)运动到点B,则DC+BC=2 ,DM+MB=
,DM+MB=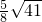 +
+ ,因为P、Q两点的运动速度相同再比较DC+BC和DM+MB的大小即可知道谁先到达点B.
,因为P、Q两点的运动速度相同再比较DC+BC和DM+MB的大小即可知道谁先到达点B.

科目:初中数学 来源: 题型:
 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=| 4 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com