
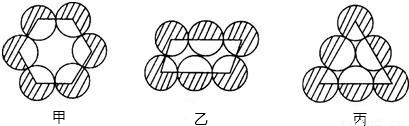
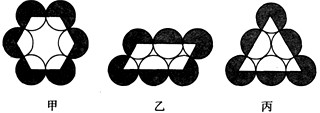
如图,有六个等圆按甲、乙、丙三种方法摆放,使相邻两圆互相外切,圆心连线分别构成正六边形、平行四边形、正三角形.圆心连线构成图形外侧的六个扇形
(阴影部分)的面积之和依次记为S、P、Q,则
S>P>Q
S>Q>P
S>P=Q
S=P=Q
|
分析:由于三个图形中的阴影部分都是由一些扇形组成的,因此要比较三个图形中的阴影部分的面积大小,可以直接运用公式 S=正六边形中所有阴影部分的圆心角的度数之和为 360°×6-(6-2)×180°=1440°;平行四边形中所有阴影部分的圆心角的度数之和为360°×6-(4-2)×180°-2×180°=1440°;正三角形中所有阴影部分的圆心角的度数之和为360°×6-(3-2)×180°-3×180°=1440°.可见所有扇形的圆心角的度数之和均相等.故选D.思维拓展:如果比较图中空白部分的扇形面积,答案又是什么呢? (请同学们自己完成)点评:在上述问题中,我们将三个图形中的扇形拼凑在一起,使复杂问题简单化. |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:第3章《圆》中考题集(69):3.7 弧长及扇形的面积(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:第3章《圆》常考题集(31):3.7 弧长及扇形的面积(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:河北省同步题 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com