
 如图,有一段斜坡BC长为30米,坡角∠CBD=30°,为方便车辆通行,
如图,有一段斜坡BC长为30米,坡角∠CBD=30°,为方便车辆通行, 解:(1)在Rt△BCD中,∵∠CDB=90°,∠CBD=30°,BC=30,
解:(1)在Rt△BCD中,∵∠CDB=90°,∠CBD=30°,BC=30, BC=15.
BC=15. =15
=15 ,
, .
.  )米.
)米.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
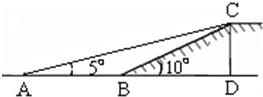 18、如图,有一段斜坡BC长为10米,坡角∠CBD=10°,为使残疾人的轮椅车通行更省力,现准备把坡角降为5°.
18、如图,有一段斜坡BC长为10米,坡角∠CBD=10°,为使残疾人的轮椅车通行更省力,现准备把坡角降为5°.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•湛江模拟)如图,有一段斜坡BC长为30米,坡角∠CBD=30°,为方便车辆通行,
(2012•湛江模拟)如图,有一段斜坡BC长为30米,坡角∠CBD=30°,为方便车辆通行,查看答案和解析>>
科目:初中数学 来源: 题型:
 现准备把坡角降为5°.
现准备把坡角降为5°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com