Question

如图（1），△ABC是等边三角形．E是AC边上的一动点，以BE为边在BC的同侧作等边△DBE．连接AD．

（1）说明：AD∥BC；
（2）若将（1）中的等边△ABC和等边△DBE改成两个等腰三角形，且它们的顶角∠BAC和顶角∠BDE相等．是否仍有AD∥BC？证明你的结论．

Answer 1

（1）解：∵△ABC和△BDE都为等边三角形，
∴∠ABC=∠DBE=60°，BD=BE，BA=BC，
∴∠DAB+∠ABE=60°，∠CBE+∠ABE=60°，
∴∠DAB=∠CBE，
在△ABD和△CBE中，
∵，
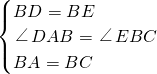
∴△ABD≌△CBE（SAS），
∴∠BAD=∠C=60°，
∴∠BAD=∠ABC=60°，
∴AD∥BC；

（2）结论仍然成立，理由为：
证明：∵△ABC和△DBE为两个等腰三角形，且它们的顶角∠BAC=∠BDE，
∴∠ABC=∠DBE，
∴∠DBE-∠ABE=∠ABC-∠ABE，即∠DBA=∠CBE，
∴△ABC∽△DBE，
∴=，
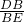
∴△ABD∽△CBE，
∴∠BAD=∠C，
又∵∠ABC=∠C，
∴∠BAD=∠ABC，
∴AD∥BC．
分析：（1）由三角形ABC与三角形BDE都为等边三角形，得到∠ABC=∠DBE=60°，BD=BE，BA=BC，利用等式的性质得到∠DBA=∠EBC，利用SAS得出三角形ABD与三角形BCE全等，利用全等三角形的对应角相等得到∠BAD=∠C=60°，而∠ABC=60°，可得出一对内错角相等，利用内错角相等两直线平行即可得证；
（2）若将（1）中的等边△ABC和等边△DBE改成两个等腰三角形，且它们的顶角∠BAC和顶角∠BDE相等．仍有AD∥BC，理由为：由两顶角相等，得到两底角，得到两等腰三角形相似，由相似得比例，再利用等式的性质得到∠DBA=∠EBC，利用两对对应边成比例且夹角相等的两三角形相似得到∠BAD=∠C，而等腰三角形两底角相等，等量代换得到一对内错角相等，利用内错角相等两直线平行即可得证．
点评：此题考查了全等三角形的判定与性质，相似三角形的判定与性质，等腰三角形的性质，以及等边三角形的性质，熟练掌握判定与性质是解本题的关键．