
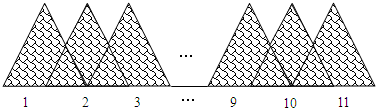
 如图,是一块玻璃纸的一部分,它由11个边长为
如图,是一块玻璃纸的一部分,它由11个边长为 的正三角形按下列方式排列:它们各自有一条边依次在同一条直线上,而且沿着这条直线,每个三角形底边的中点恰为下一个三角形的顶点,则由这11个三角形所盖住的玻璃(平面的)区域的面积是________(答案可带根号).
的正三角形按下列方式排列:它们各自有一条边依次在同一条直线上,而且沿着这条直线,每个三角形底边的中点恰为下一个三角形的顶点,则由这11个三角形所盖住的玻璃(平面的)区域的面积是________(答案可带根号).
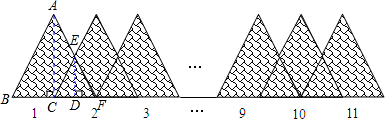 解:将第一个等边三角形向右连续平移,每次平移的距离是边长的一半;
解:将第一个等边三角形向右连续平移,每次平移的距离是边长的一半; ,
, ,
, =6,
=6,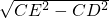 =3,
=3, ×2
×2 ×3=3
×3=3 ,
, ×4
×4 ×h=
×h= ×4
×4 ×6=12
×6=12 ,
, -3
-3 ×10=102
×10=102 .
. .
.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com