
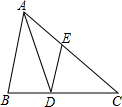
 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
分析 先设CE=3k,AC=5k,则AE=2k,根据AD为△ABC的角平分线,DE∥AB,可得AE=DE=2k,再根据△CDE∽△CBA,即可得到AB=$\frac{10}{3}$k,进而得出$\frac{AE}{AB}$的值.
解答 解:∵$\frac{CE}{AC}=\frac{3}{5}$,
∴可设CE=3k,AC=5k,则AE=2k,
∵AD为△ABC的角平分线,DE∥AB,
∴∠BAD=∠DAE=∠ADE,
∴AE=DE=2k,
∴CE:DE=3:2,
∵DE∥AB,
∴△CDE∽△CBA,
∴$\frac{CE}{DE}=\frac{CA}{BA}$,即$\frac{3}{2}=\frac{5k}{AB}$,
∴AB=$\frac{10}{3}$k,
∴$\frac{AE}{AB}$=$\frac{2k}{\frac{10}{3}k}$=$\frac{3}{5}$,
故选:D.
点评 本题主要考查了相似三角形的判定与性质,解题时注意:相似三角形的对应边成比例.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:选择题
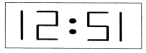 墙上有一面镜子,镜子对面的墙上有一个数字式电子钟.如果在镜子里看到该电子钟的时间显示如图所示,那么它的实际时间是( )
墙上有一面镜子,镜子对面的墙上有一个数字式电子钟.如果在镜子里看到该电子钟的时间显示如图所示,那么它的实际时间是( )| A. | 1 2:5 1 | B. | 1 5:2 1 | C. | 1 5:5 1 | D. | 1 2:2 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
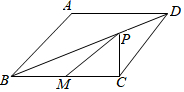 如图,菱形ABCD的边长为4cm,∠ABC=60°,且M为BC的中点,P是对角线BD上的一动点,则PM+PC的最小值为( )
如图,菱形ABCD的边长为4cm,∠ABC=60°,且M为BC的中点,P是对角线BD上的一动点,则PM+PC的最小值为( )| A. | 4 cm | B. | $\sqrt{3}$cm | C. | 2$\sqrt{5}$cm | D. | 2$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
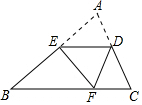 如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若△ABC的周长为12$\sqrt{3}$,则△DEF的周长是( )
如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若△ABC的周长为12$\sqrt{3}$,则△DEF的周长是( )| A. | 5$\sqrt{3}$cm | B. | 6$\sqrt{3}$cm | C. | 5cm | D. | 4$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
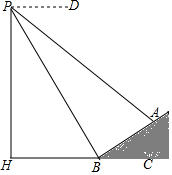 如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.
如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为( )米.| A. | 200$\sqrt{3}$ | B. | 200 | C. | 100$\sqrt{3}$ | D. | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com