Question

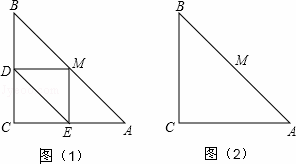
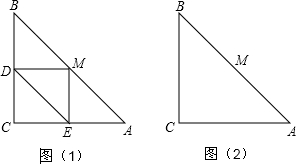
如图（1），将一直角三角形的直角顶点M放在腰长为4的等腰直角三角形ABC斜边的中点，另两条直角边分别与线段BC，AC交于D，E两点，当绕着直角顶点M旋转时，该直角三角形两直角边与△ABC两直角边的交点位置随之发生变化．有两位同学提出各自的判断：甲，△MDE的形状不会发生变化；乙，四边形MECD的面积不会发生变化．你认为这两位同学的判断是否正确？请在图（2）中作出旋转后的图形，并说明理由．

试题答案 练习册答案 在线课程 考点：	等腰直角三角形；全等三角形的判定与性质．.
分析：	连接CM，根据等腰直角三角形的性质可得BM=CM，∠ACM=∠B=45°，再根据同角的余角相等求出∠BMD=∠CME，再利用“角边角”证明△BMD和△CME全等，根据全等三角形对应边相等可得DM=DE，从而得到△MDE是等腰直角三角形，再求出四边形MECD的面积等于△BCM的面积．
解答：	解：甲乙两位同学的判断都正确． 如图，连接CM，∵M是等腰直角△ABC的中点， ∴BM=CM，∠ACM=∠B=45°，∠CMB=90°， ∵∠DME=90°， ∴∠BMD+∠CMD=90°， ∠CME+∠CMD=90°， ∴∠BMD=∠CME， 在△BMD和△CME中，， ∴△BMD≌△CME（ASA）， ∴MD=ME， ∴△MDE是等腰直角三角形， 因此，△MDE的形状不会发生变化，故甲的说法正确； S四边形MECD=S△CME+S△CME=S△BMD+S△CME=S△CBCM，不变，所以，乙的说法正确， 综上所述，甲乙两位同学的判断都正确．
点评：	本题考查了等腰直角三角形的性质，全等三角形的判定与性质，熟记性质并作出辅助线构造出全等三角形是解题的关键．

Answer 1

考点：