
 时,sinB=
时,sinB= ;
; 时,sinB=
时,sinB= (提示:
(提示: =
= );
); 时,sinB=
时,sinB= .
. 时,sinB的值等于______
时,sinB的值等于______ 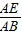 的分母加1即是sinB的分母,sinB的分子是2乘以
的分母加1即是sinB的分母,sinB的分子是2乘以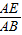 的分母的算术平方根,根据规律直接写出答案即可;
的分母的算术平方根,根据规律直接写出答案即可; ,再设EM=k,则BN=nk,作EH∥MN交BC于H,则HN=EM=k.
,再设EM=k,则BN=nk,作EH∥MN交BC于H,则HN=EM=k. •k,则sinB=
•k,则sinB=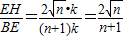 .
. 解:(1)
解:(1)

 (n是大于1的自然数)
(n是大于1的自然数) .
. .
. •k
•k .
. .
. MN=
MN= ,OA=AM+MO=
,OA=AM+MO=
 •k
•k .
.

 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源:2002年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
 )和(0,-
)和(0,- ).点P(x,y)在抛物线的顶点M的右侧的半支上(包括顶点M),在x轴上有一点C使△OPC是等腰三角形,OP=PC.
).点P(x,y)在抛物线的顶点M的右侧的半支上(包括顶点M),在x轴上有一点C使△OPC是等腰三角形,OP=PC.查看答案和解析>>
科目:初中数学 来源:2002年北京市朝阳区中考数学试卷(解析版) 题型:解答题
 )和(0,-
)和(0,- ).点P(x,y)在抛物线的顶点M的右侧的半支上(包括顶点M),在x轴上有一点C使△OPC是等腰三角形,OP=PC.
).点P(x,y)在抛物线的顶点M的右侧的半支上(包括顶点M),在x轴上有一点C使△OPC是等腰三角形,OP=PC.查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《锐角三角函数》(02)(解析版) 题型:选择题



查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《图形的相似》(06)(解析版) 题型:解答题
 ,EH-HF=2.设∠ACB=a,tana=
,EH-HF=2.设∠ACB=a,tana= ,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.
,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com