
分析 通过解方程$\frac{x-1}{2}$+1=$\frac{x}{3}$得到x=-3,然后根据题意得到关于x的方程$\frac{3}{4}$+8x=7k+6x的解是x=0,将其代入该方程列出关于k的新方程,再通过解新方程求得k的值即可.
解答 解:解方程$\frac{x-1}{2}$+1=$\frac{x}{3}$,得
x=-3.
所以关于x的方程$\frac{3}{4}$+8x=7k+6x的解是x=0,
把x=0代入,得
$\frac{3}{4}$=7k,
解得k=$\frac{3}{28}$.
点评 本题考查了一元一次方程的解的定义.定义:使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “经过有交通信号的路口,遇到红灯,”是必然事件 | |
| B. | 已知某篮球运动员投篮投中的概率为0.6,则他投10次一定可投中6次 | |
| C. | 处于中间位置的数一定是中位数 | |
| D. | 方差越大数据的波动越大,方差越小数据的波动越小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
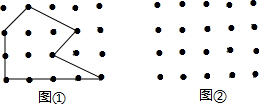
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
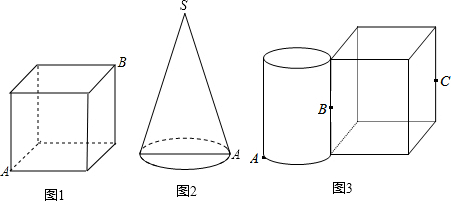
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
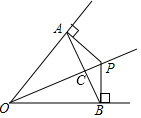 如图,OP平分∠AOB,PA⊥OA于A,PB⊥OB于B,连结AB交OP于C,给出下列结论:
如图,OP平分∠AOB,PA⊥OA于A,PB⊥OB于B,连结AB交OP于C,给出下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
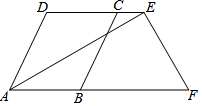 已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,∠DEA=30°,AE⊥EF,垂足为E.
已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,∠DEA=30°,AE⊥EF,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
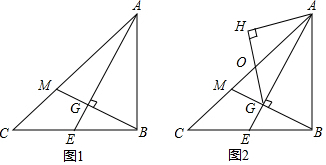
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com