
 如图为某学校一块空地,为了绿化环境,学校打算利用这块空地种植花草,已知AB⊥BC,CD⊥BC,∠D=30°,AB=$\frac{1}{4}$CD=$\sqrt{6}$m,BC=3$\sqrt{2}$m,试求这块空地的周长和面积.
如图为某学校一块空地,为了绿化环境,学校打算利用这块空地种植花草,已知AB⊥BC,CD⊥BC,∠D=30°,AB=$\frac{1}{4}$CD=$\sqrt{6}$m,BC=3$\sqrt{2}$m,试求这块空地的周长和面积. 分析 过点A作AE⊥CD于点E,则四边形ABCD分割为直角三角形AED和矩形ABCE两部分,求出AD的长则周长可求出,再利用梯形的面积公式可求出四边形其面积.
解答 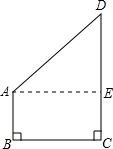 解:过点A作AE⊥CD于点E,
解:过点A作AE⊥CD于点E,
∵AB⊥BC,CD⊥BC,
∴四边形ABCE是矩形,
∴AE=BC=3$\sqrt{2}$m,
∵∠D=30°,
∵AE=$\frac{1}{2}$AD,
∴AD=6$\sqrt{2}$m,
∴四边形ABCD的周长=AB+BC+CD+AD=$\sqrt{6}$+3$\sqrt{2}$+4$\sqrt{6}$+6$\sqrt{2}$=(5$\sqrt{6}$+9$\sqrt{2}$)m;
四边形ABCD的面积=$\frac{(AB+DC)•BC}{2}$=$\frac{(\sqrt{6}+4\sqrt{6})×3\sqrt{2}}{2}$=36$\sqrt{2}$cm2.
点评 本题考查了勾股定理的应用,解题的关键是过点A作AE⊥CD于点E,则四边形ABCD分割为直角三角形AED和矩形ABCE两部分,利用直角三角形的性质和矩形的性质解答题目.


科目:初中数学 来源: 题型:选择题
| A. | 3x+2y=5 | B. | y2+6y+5=0 | C. | $\frac{1}{3}x=\frac{1}{x}$ | D. | 3x-4=7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在方格纸中,选择标有序号的一个小正方形涂黑,与图中阴影构成中心对称图形,涂黑的小正方形序号为②;若与图中阴影构成轴对称图形,涂黑的小正方形序号为⑤或⑥或⑦.
在方格纸中,选择标有序号的一个小正方形涂黑,与图中阴影构成中心对称图形,涂黑的小正方形序号为②;若与图中阴影构成轴对称图形,涂黑的小正方形序号为⑤或⑥或⑦.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD中,∠C=40°,∠B=∠D=90°,E、F分别是BC、DC上的一点,当△AEF的周长最小时,∠EAF的度数为100°.
如图,四边形ABCD中,∠C=40°,∠B=∠D=90°,E、F分别是BC、DC上的一点,当△AEF的周长最小时,∠EAF的度数为100°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com