

 BC,∠GAC=∠H<∠HAG,
BC,∠GAC=∠H<∠HAG,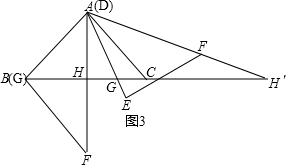
 BC时,G为BC的中点,H与C重合,△AGH是等腰三角形,
BC时,G为BC的中点,H与C重合,△AGH是等腰三角形,
 ,
, BC时,由(1)△AGC∽△HGA,
BC时,由(1)△AGC∽△HGA, ,
, 或
或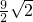 .
. BC,②CG=
BC,②CG= BC时,③CG>
BC时,③CG> BC时分别得出即可.
BC时分别得出即可.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
 27、如图,已知RT△ABC与RT△DEF不相似,其中∠C、∠F为直角,能否分别将这两个三角形各分割成两个三角形,使△ABC所分的每个三角形与△DEF所分成的每个三角形分别对应相似?若能,请设计出一种分割方案.
27、如图,已知RT△ABC与RT△DEF不相似,其中∠C、∠F为直角,能否分别将这两个三角形各分割成两个三角形,使△ABC所分的每个三角形与△DEF所分成的每个三角形分别对应相似?若能,请设计出一种分割方案.查看答案和解析>>
科目:初中数学 来源: 题型:
 20、已知:△ABC与△CDE都是顶角为36°的等腰三角形,BC=CD,AC与BD交于F,且B、C、E三点共线.
20、已知:△ABC与△CDE都是顶角为36°的等腰三角形,BC=CD,AC与BD交于F,且B、C、E三点共线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com