
【题目】共享单车作为一种低碳、时尚、绿色的出行方式,它俨然成为市民出行的“新宠”.某公司准备安装A款共享单车,完成5760辆该款共享单车投入市场运营的计划.由于抽调不出足够的熟练工人完成安装,公司准备招聘一批新工人,将他们培训到能独立进行安装后上岗。生产开始后发现:4名熟练工人和5名新工人每天共安装88辆共享单车;2名熟练工人每天安装的共享单车数与3名新工人每天安装的共享单车数一样多.
(1)求每名熟练工人和新工人每天分别可以安装多少辆共享单车?
(2)若公司招聘m名新工人,使得招聘的新工人和抽调的熟练工人刚好一个月(30天)完成安装任务,已知工人们安装的共享单车中不能正常投入运营的占4%,且招聘的新工人数比抽调的熟练工人数少,求m的值.
【答案】(1)每名熟练工人每天可以安装12辆共享单车,新工人每天可以安装8辆共享单车.(2)1,4,7.
【解析】分析:(1)设每名熟练工每月可以安装x辆电动车,新工人每月分别安装y辆电动汽车,根据4名熟练工人和5名新工人每天共安装88辆共享单车;2名熟练工人每天安装的共享单车数与3名新工人每天安装的共享单车数一样多,两个等量关系列出方程组,然后求解即可;
(2)设抽调n名熟练工人,根据一年的安装任务列出方程整理,用m表示出n,然后根据人数m是整数讨论求解即可.
详解:(1)设每名熟练工人每天可以安装x辆共享单车,新工人每天可以安装y辆共享单车.
![]() 解得
解得![]()
答:每名熟练工人每天可以安装12辆共享单车,新工人每天可以安装8 辆共享单车.
(2)设抽调n名熟练工人(n>m),需安装5760÷(1-4%)=6000(辆),则(8m+12n)×30=6000 化简得:2m +3n =50
![]() .∵m、n为正整数且n>m,∴m=1,4,7
.∵m、n为正整数且n>m,∴m=1,4,7


科目:初中数学 来源: 题型:
【题目】某人因需要经常去复印资料,甲复印社按A4纸每10页2元计费,乙复印社则按A4纸每10页1元计费,但需按月付一定数额的承包费. 两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题:
(1)乙复印社要求客户每月支付的承包费是 元.
(2)当每月复印 页时,两复印社实际收费相同.
(3)如果每月复印页在250页左右时,应选择哪一个复印社?请简单说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
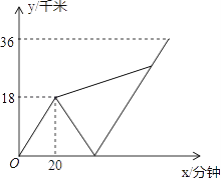
【题目】甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为t(分钟).y甲、y乙与x之间的函数图象如图所示,则乙返回到学校时,甲与学校相距________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,矩形OABC的长OA= ![]() ,宽OC=1,将△AOC沿AC翻折得△APC.
,宽OC=1,将△AOC沿AC翻折得△APC.
(1)求∠PCB的度数;
(2)若P,A两点在抛物线y=﹣ ![]() x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
(3)(2)中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点,N是y轴上的点,以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园. 如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是____,因变量是______;
(2)小明家到滨海公园的路程为____ km,小明在中心书城逗留的时间为____ h;
(3)小明出发______小时后爸爸驾车出发;
(4)图中A点表示___________________________________;
(5)小明从中心书城到滨海公园的平均速度为______km/h,小明爸爸驾车的平均速度为______km/h;(补充;爸爸驾车经过______追上小明);
(6)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D、E、F分别在三边上,E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△GEC=3,S△GDC=4,则△ABC的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米. 
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系. ①求抛物线的解析式; ②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分. ①求圆的半径;②要使高为3米的船通过,则其宽度须不超过多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若∠A=30°,AB=AC,则∠BDE的度数为( )

A. 67.5° B. 52.5° C. 45° D. 75°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com