
 上,AB边在直线
上,AB边在直线 上.
上.
 上,AB边在直线
上,AB边在直线 上,所以O(0,0),A是两直线的交点.将两直线的解析式联立,得到方程组,解之即可得到A的坐标
上,所以O(0,0),A是两直线的交点.将两直线的解析式联立,得到方程组,解之即可得到A的坐标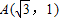 ,利用菱形的对称性即可得到B,C点的坐标.
,利用菱形的对称性即可得到B,C点的坐标. ,整理即可得到所要求的解析式.
,整理即可得到所要求的解析式.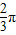 ,设截下的⊙Q符合条件,其半径为R,则
,设截下的⊙Q符合条件,其半径为R,则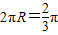 ,所以
,所以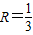 ,由(2)知,此时OA=y=2,则⊙Q的半径大于R,能截下一个圆,使得它与扇形OAC刚好围成一个圆锥,从而求此圆的面积.
,由(2)知,此时OA=y=2,则⊙Q的半径大于R,能截下一个圆,使得它与扇形OAC刚好围成一个圆锥,从而求此圆的面积.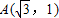 ,
,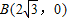 ,C(
,C(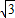 ,-1);(2分)
,-1);(2分)
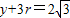 ,
,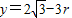 .
.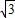 -3r>0,
-3r>0,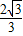 ,
,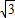 ,1)
,1) -3r≤2,
-3r≤2, ≤r,
≤r,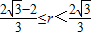 .
.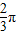 .
.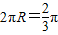 .
.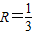 .
.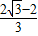 >
> ,
,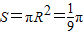 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2010年中考数学十校联考模拟试卷(解析版) 题型:解答题
 上,AB边在直线
上,AB边在直线 上.
上.
查看答案和解析>>
科目:初中数学 来源:2010年四川省宜宾市横江片区春季期半期检测数学试卷(解析版) 题型:解答题
| 行驶时间 (时) | 1 | 2 | 2.5 | |
| 余油量 (升) | 100 | 80 | 60 | 50 |
查看答案和解析>>
科目:初中数学 来源:2010年北京市朝阳区中考数学模拟试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年北京市宣武区中考数学二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com