



分析 (1)根据 HL或AAS,可以知道Rt△ABC≌Rt△DEF;
(2)如图1所示:以C或F为圆心,BC的长为半径画弧,分别交AM,DN与B,E,则△ABC与△DEF不全等;
(3)当BC≥CA时,也能使△ABC≌△DEF,①当BC=CA时,△ABC和△DEF是有一个底角相等的等腰三角形,根据AAS易证两三角形全等,②当BC>CA时,在射线AM上取点B,使BC>CA,连接BC,以F为圆心,CB长为半径画弧交射线DN于点E,连接FE,则BC=EF,过点F作FG⊥DE于点G,证明△CAH≌△FDG(AAS),得到CH=FG,通过Rt△CBH≌Rt△FEG(HL),得到∠CBA=∠FED,证得△ABC≌△DEF(AAS).
解答 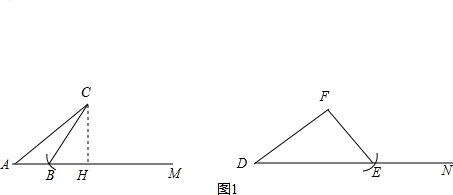 解:(1)解:在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D,根据 HL或(AAS),可以知道Rt△ABC≌Rt△DEF.
解:(1)解:在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D,根据 HL或(AAS),可以知道Rt△ABC≌Rt△DEF.
故答案为;HL或AAS;
(2)如图1所示:
(3)当BC≥CA时,也能使△ABC≌△DEF,
证明:①当BC=CA时,△ABC和△DEF是有一个底角相等的等腰三角形,
根据AAS易证两三角形全等,
②当BC>CA时,在射线AM上取点B,使BC>CA,连接BC,
以F为圆心,CB长为半径画弧交射线DN于点E,连接FE,则BC=EF,
过点F作FG⊥DE于点G,
在△CAH和△FDG中,$\left\{\begin{array}{l}{∠A=∠D}\\{∠AHC=∠DGF}\\{AC=DF}\end{array}\right.$,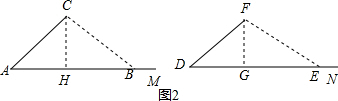
∴△CAH≌△FDG(AAS),
∴CH=FG,
在Rt△CBH和Rt△FEG中,$\left\{\begin{array}{l}CH=FG\\ CB=FE\end{array}\right.$
∴Rt△CBH≌Rt△FEG(HL),
∴∠CBA=∠FED,
在△ABC和△EFD中,$\begin{array}{l}\left\{\begin{array}{l}∠CBA=∠FED\\∠A=∠D\\ AC=DF\end{array}\right.\end{array}$
∴△ABC≌△DEF(AAS).
点评 本题考查了全等三角形的判定与性质,应用与设计作图,熟练掌握三角形全等的判定方法是解题的关键,阅读量较大,审题要认真仔细.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
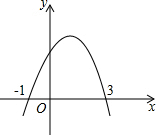 如图,抛物线y=ax2+bx+c交x轴于(-1,0)、(3,0)两点,则下列判断中,正确的是( )
如图,抛物线y=ax2+bx+c交x轴于(-1,0)、(3,0)两点,则下列判断中,正确的是( )| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 周末,东东一家三口人开车去距家15km的二克山公园游玩,行驶10min后,接到爷爷奶奶的电话,也要一同前往,于是妈妈下午步行前往,东东和爸爸开车按原路返回接爷爷奶奶,接到爷爷奶奶后,开车前往公园,在距离公园3.75km处追上妈妈并同车前往公园,若汽车速度始终保持不变,设汽车与家相距y1(单位:km),妈妈与家相距y2(单位:km),汽车离开家的时间为x(单位:min),y1、y2与x之间的函数图象如图所示,结合图象解答下列问题:
周末,东东一家三口人开车去距家15km的二克山公园游玩,行驶10min后,接到爷爷奶奶的电话,也要一同前往,于是妈妈下午步行前往,东东和爸爸开车按原路返回接爷爷奶奶,接到爷爷奶奶后,开车前往公园,在距离公园3.75km处追上妈妈并同车前往公园,若汽车速度始终保持不变,设汽车与家相距y1(单位:km),妈妈与家相距y2(单位:km),汽车离开家的时间为x(单位:min),y1、y2与x之间的函数图象如图所示,结合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
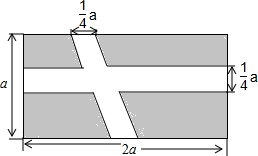 小林负责一块宽为a,长为2a的长方形草坪铺设鹅卵石小路供游人行走,他计划铺设两条宽为$\frac{1}{4}$a的鹅卵石(如图所示),其余部分全部种草
小林负责一块宽为a,长为2a的长方形草坪铺设鹅卵石小路供游人行走,他计划铺设两条宽为$\frac{1}{4}$a的鹅卵石(如图所示),其余部分全部种草查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com