
 AC;
AC;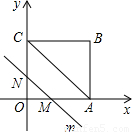
 AC时,有两种情况,①MN是△OAC的中位线,此时OM=
AC时,有两种情况,①MN是△OAC的中位线,此时OM= OA=2,因此t=2;
OA=2,因此t=2; OA=6,因此t=6;
OA=6,因此t=6;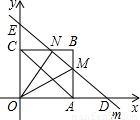 解:(1)(4,0),(0,3);
解:(1)(4,0),(0,3); AC时,有两种情况,
AC时,有两种情况, OA=2,因此t=2;
OA=2,因此t=2; AB=
AB= ,OA=4,
,OA=4, =
=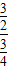 =2
=2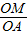 =
=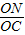 ,
,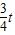 ,S=
,S= t2
t2 ∴AD=t-4
∴AD=t-4 (t-4)
(t-4)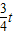
 BM=8-t
BM=8-t (t-4)-
(t-4)- (8-t)(6-
(8-t)(6-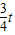 )-
)-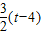 =
=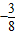 t2+3t
t2+3t BN=6-
BN=6-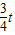 ,
, (t-4)
(t-4) t2的开口向上,在对称轴t=0的右边,S随t的增大而增大
t2的开口向上,在对称轴t=0的右边,S随t的增大而增大 ×42=6;(11分)
×42=6;(11分)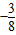 t2+3t的开口向下,它的顶点是(4,6),
t2+3t的开口向下,它的顶点是(4,6),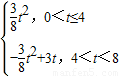


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
 (2008•临夏州)如图,小红和小丽在操场上做游戏,她们先在地上画出一个圆圈,然后站在距圆圈5米的地方向圆圈内投小石子,则投一次就正好投到圆圈内是( )
(2008•临夏州)如图,小红和小丽在操场上做游戏,她们先在地上画出一个圆圈,然后站在距圆圈5米的地方向圆圈内投小石子,则投一次就正好投到圆圈内是( )查看答案和解析>>
科目:初中数学 来源: 题型:
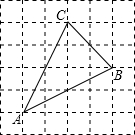 (2008•临夏州)如图,网格小正方形的边长都为1.在△ABC中,试画出三边的中线(顶点与对边中点连结的线段),然后探究:三条中线位置的关系,以及三条中线所成的线段长度之间的关系,写出你发现的一般结论.
(2008•临夏州)如图,网格小正方形的边长都为1.在△ABC中,试画出三边的中线(顶点与对边中点连结的线段),然后探究:三条中线位置的关系,以及三条中线所成的线段长度之间的关系,写出你发现的一般结论.查看答案和解析>>
科目:初中数学 来源:2010年中考数学考前知识点回归+巩固 专题11 一次函数(解析版) 题型:解答题
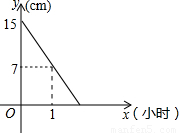
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com