
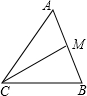
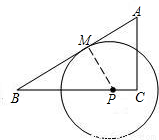
 如图,设△ABC的两边AC与BC之和为a,M是AB的中点,MC=MA=5,则a的取值范围是
如图,设△ABC的两边AC与BC之和为a,M是AB的中点,MC=MA=5,则a的取值范围是| 2 |
| 2 |
| a2-100 |
| 2 |
|
| a2-100 |
| 2 |
| a2-100 |
| 2 |
| a2-100 |
| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
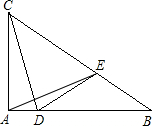 点E沿BC从B向C运动,速度为2cm/秒.动点E到达点C时运动终止.连接DE、CD、AE.
点E沿BC从B向C运动,速度为2cm/秒.动点E到达点C时运动终止.连接DE、CD、AE.查看答案和解析>>
科目:初中数学 来源:2009年福建省三明市尤溪一中高一保送生数学模拟卷(一)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009年浙江省温州市永嘉县中考数学二模试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年福建省三明市大田二中自主招生数学模拟试卷(3)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com