Question

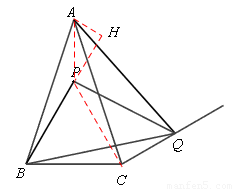
在△ABC中，AB=AC，∠BAC＜60°，把线段BC绕点B逆时针旋转60°至BP；如图所示位置有∠ABQ=60°，∠BCQ=150°．

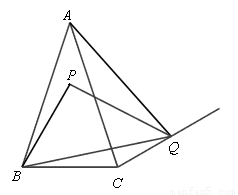
（1）若∠BAC=30°，则∠ABP=       度；若∠BAC=α，则∠ABP=           （用α表示）；

（2）求证：△ABQ为等边三角形；

（3）四边形CBPQ的面积为1，求△ABC的面积．

 

Answer 1

【答案】

（1）15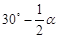，；（2）证明见解析；（3）1.

【解析】

试题分析：（1）若∠BAC=30°，一方面在△ABC中，AB=AC，可得∠ABC=75°，另一方面由旋转的性质知∠CBP=60°，因而∠ABP=15°；若∠BAC=α，同上可得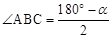，因而由∠BAC＜60°可得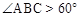，所以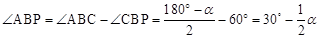；（2）连接CP，AP，由已知和旋转的性质，通过证明△ABP≌△ACP（SSS）和△ABP≌△QBC（ASA）来证明△ABQ为等边三角形；（3）通过转换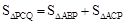，可得.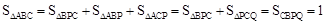

试题解析：（1）15；.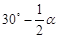

（2）如图，连接CP，AP，

由旋转的性质知BC=BP，∠CBP=60°，∴△BCP为等边三角形. ∴BP=CP，∠BPC=60°.

在△ABP和△ACP中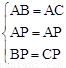，∵，∴△ABP≌△ACP（SSS）. ∴.

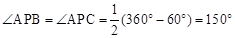又∵∠BCQ=150°，∴ .

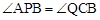在△ABP和△QBC中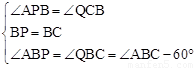，∵，∴△ABP≌△QBC（ASA）. ∴BA=BQ.

∴△ABQ为等边三角形.

（3）如图，过点A作AH⊥BP交BP的延长线于点H，则

由（2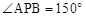）得，∴. ∴.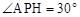

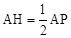由（2）△ABQ为等边三角形得，∴. ∴.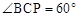

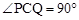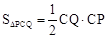由（2）得，∴.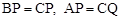

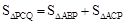又∵，∴.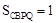

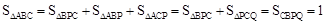考点：1. 旋转的性质；2.等腰三角形的性质；3.三角形内角和定理；4.等边三角形的判定和性质；5.全等三角形的判定和性质；6.转换思想的应用.