Question

3．为解决都市停车难的问题，计划在一段长为56米的路段规划出如图所示的停车位，已知每个车位是长为5米，宽为2米的矩形，且矩形的宽与路的边缘成45°角，则该路段最多可以划出18个这样的停车位．（取$\sqrt{2}$=1.4，结果保留整数）

Answer 1

分析 如图，根据三角函数可求BC，AB，设至多可划x个车位，依题意可列不等式2$\sqrt{2}$x+（5-2）×$\frac{\sqrt{2}}{2}$≤56，解不等式即可求解．

解答 解：如图，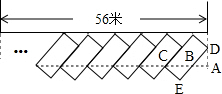

∵CE=2，DE=5，且∠BCE=∠CBE=∠ABD=∠ADB=45°，
∴BE=CE=2，BD=DE-BE=3，
∴BC=2÷sin45°=2$\sqrt{2}$，AB=（5-2）×sin45°=（5-2）×$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{2}$，
设至多可划x个车位，依题意可列不等式
2$\sqrt{2}$x+$\frac{3\sqrt{2}}{2}$≤56，
整理，得：2x+$\frac{3}{2}$≤28$\sqrt{2}$，
x≤14$\sqrt{2}$-$\frac{3}{4}$，
将$\sqrt{2}$=1.4代入不等式得，x≤18.85，
因为是正整数，所以x=18，
所以这个路段最多可以划出18个这样的停车位．
故答案为：18．

点评 考查了解直角三角形的应用，主要是三角函数及运算，关键把实际问题转化为数学问题加以计算．