
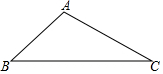
 如图,BC=50,∠ABC=45°,∠ACB=30°,求点A到BC的距离.
如图,BC=50,∠ABC=45°,∠ACB=30°,求点A到BC的距离. 分析 作AD⊥BC与D,设公共直角边为未知数,利用特殊的角的三角函数表示出BD、CD,相加等于BC的长度即可求得点A到BC的距离.
解答 解:如图过点A作AD⊥BC于点D,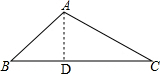
则∠ADB=∠ADC=90°,
设AD=x,
∵∠ABC=45°,∠ACB=30°,
∴BD=AD=x,CD=$\frac{AD}{tan∠ACD}$=$\frac{x}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$x,
则x+$\sqrt{3}$x=50,
解得:x=25$\sqrt{3}$-25,即点A到BC的距离为25$\sqrt{3}$-25.
点评 此题考查了解直角三角形的应用,解此题的关键是把实际问题抽象到直角三角形中,利用公共边及特殊的三角函数求解.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:填空题
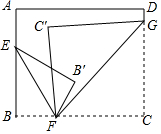 如图所示.将一张长方形纸片分别沿着EF,FG对折,使点B落在点B′,点C落在C′(B′在C′的右侧),若∠B′FC′=28°,则∠EFG的度数为104°.
如图所示.将一张长方形纸片分别沿着EF,FG对折,使点B落在点B′,点C落在C′(B′在C′的右侧),若∠B′FC′=28°,则∠EFG的度数为104°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
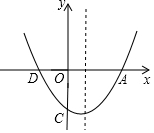 如图,已知抛物线的顶点为(1,-$\frac{27}{8}$),与y轴交点C(0,-3),与x轴的交点为A,D(A在D的右侧).
如图,已知抛物线的顶点为(1,-$\frac{27}{8}$),与y轴交点C(0,-3),与x轴的交点为A,D(A在D的右侧).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
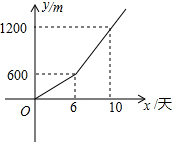 (1)在学习一次函数的图象时,我们根据函数图象的定义,按画函数图象的基本步骤,画出一次函数的图象,请您按画函数图象的基本步骤画出函数y=2x+4的图象.
(1)在学习一次函数的图象时,我们根据函数图象的定义,按画函数图象的基本步骤,画出一次函数的图象,请您按画函数图象的基本步骤画出函数y=2x+4的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
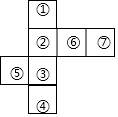 小刚在纸上画了一个长方体的展开图,展开图由长方形和正方形构成,淘气的小明在图上又添加了一个四边形,并把这7个面任意标上了①~⑦的序号(如图).
小刚在纸上画了一个长方体的展开图,展开图由长方形和正方形构成,淘气的小明在图上又添加了一个四边形,并把这7个面任意标上了①~⑦的序号(如图).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com