
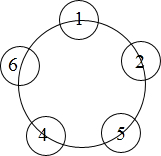
 将数字1,2,5,4,6填入图中的小圆圈中.从1开始顺时针依次数两个数字可产生5个两位数12,25,54,46和61.从1开始逆时针依次数两个 数字可产生另5个两位数16,64,45,52和21.
将数字1,2,5,4,6填入图中的小圆圈中.从1开始顺时针依次数两个数字可产生5个两位数12,25,54,46和61.从1开始逆时针依次数两个 数字可产生另5个两位数16,64,45,52和21. 表示为10a+b,其它数依此类推,利用完全平方公式分别计算等式左右两边,并进行比较,证明结论;
表示为10a+b,其它数依此类推,利用完全平方公式分别计算等式左右两边,并进行比较,证明结论;

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com