
分析 (1)关系式为:190≤甲种汽车总进价+乙种汽车总进价≤200,根据此不等关系列不等式组求解即可;
(2)利润=甲种汽车数量×(14.5-12)+乙种汽车数量×(10-8),整理后按(1)中自变量的取值算出最大利润;
(3)用最大利润45万元来进货,用最大利润进货,没有总件数限制,但要考虑尽量把钱用完.分以下五种情况讨论,通过计算比较即可.①全进甲,能购买3辆;②全进乙,能购买5辆;③甲进1辆,同时乙进4辆;④甲进2辆,同时乙进2辆;⑤甲进3辆,同时乙进1辆.
解答 解:(1)设购进甲种汽车x辆,则购进乙种汽车(20-x)辆.
由题意195≤12x+8(20-x)≤205,
解得$\frac{35}{4}$≤x≤$\frac{45}{4}$,
∵x为非负整数,
∴x取9,10,11,
有三种进货方案:
①购甲种汽车9辆,乙种汽车11辆;
②购甲种汽车10辆,乙种汽车10辆;
③购甲种汽车11辆,乙种汽车9辆.
(2)设利润为w元,
则w=x×(14.5-12)+(20-x)×(10-8)=0.5x+40,
因为0.5>0,所以函数w随x的增大而增大,
结合(1)的结果可知,
∴购甲种汽车11辆,乙种汽车9辆时,可获得最大利润,最大利润是45.5万元.
(3)①全进甲,能购买3辆,利润为(14.5-12)×3=7.5万元;
②全进乙,能购买5辆,利润(10-8)×5=10万元;
③甲进1辆,同时乙进4辆,利润(14.5-12)×1+(10-8)×4=10.5万元;
④甲进2辆,同时乙进2辆,利润为2.5×2+2×2=9万元;
⑤甲进3辆,同时乙进1辆,2.5×3+2×1=9.5万元;
∴甲进1辆,同时乙进4辆时,利润最大,最大利润为10.5万元.
点评 本题考查一次函数的应用,不等式的应用解决本题的关键是读懂题意,找到符合题意的不等关系式,及所求量的等量关系.要会用分类的思想来讨论问题并能用不等式的特殊值来求得方案的问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
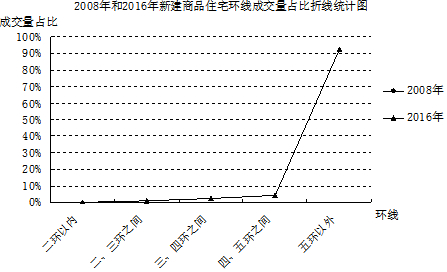
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运输单位 | 运输速度(千米/时) | 运费单价(元/吨•千米) | 装卸费用(元) |
| 汽车货运公司 | 50 | 1.8 | 2500 |
| 火车货运站 | 100 | 1.6 | 4500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
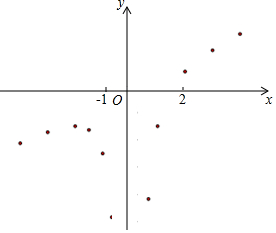 有这样一个问题:探究函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{2}$x-$\frac{2}{x^2}$的图象与性质.| x | … | -4 | -3 | -2 | -$\frac{3}{2}$ | -1 | -$\frac{2}{3}$ | $\frac{2}{3}$ | 1 | 2 | 3 | 4 | … |
| y | … | -$\frac{17}{8}$ | -$\frac{31}{18}$ | -$\frac{3}{2}$ | -$\frac{59}{36}$ | -$\frac{5}{2}$ | -$\frac{29}{6}$ | -$\frac{25}{6}$ | -$\frac{3}{2}$ | $\frac{1}{2}$ | $\frac{23}{18}$ | m | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等边三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | + | B. | - | C. | +或× | D. | -或÷ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com