
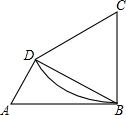
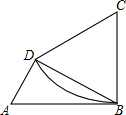
 如图,有一四边形形状的铁皮ABCD,BC=CD=12,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.则该圆锥的底面半径为________.
如图,有一四边形形状的铁皮ABCD,BC=CD=12,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.则该圆锥的底面半径为________. =
= ,
,
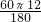 =4π,
=4π,

 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
 停止运动,△EFG也随之停止平移,设运动时间为x(s),FG的延长线交AC于H,(不考虑点P与G、F重合的情况)
停止运动,△EFG也随之停止平移,设运动时间为x(s),FG的延长线交AC于H,(不考虑点P与G、F重合的情况)查看答案和解析>>
科目:初中数学 来源:设计九年级上数学人教版 人教版 题型:044
如图,有一四边形形状的铁皮ABCD,BC=CD,AB=2AD,∠ABC=∠ADB=90°.

(1)求∠C的度数.
(2)以C为圆心,CB为半径作圆弧BD得一扇形并把它围成一圆锥侧面.若已知BC=a.求该圆锥底面半径r.
(3)在(2)中,用剩下的材料能否剪下一块整的圆面做该圆锥的底面?并说明理由.
查看答案和解析>>
科目:初中数学 来源:三点一测丛书 九年级数学 上 (江苏版课标本) 江苏版课标本 题型:044
如图,有一块四边形形状的铁皮ABCD,BC=CD,AB=2AD,∠ABC=∠ADB=90°.(1)求∠C的度数;(2)以C为圆心,CB为半径作圆弧![]() 得一扇形CBD,剪下该扇形并用它围成一圆锥的侧面,若已知BC=a,求该圆锥的底面半径;(3)在剩下的材料中,能否剪下一块整圆做该圆锥的底面?并说明理由.
得一扇形CBD,剪下该扇形并用它围成一圆锥的侧面,若已知BC=a,求该圆锥的底面半径;(3)在剩下的材料中,能否剪下一块整圆做该圆锥的底面?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,有一四边形形状的铁皮ABCD,BC=CD=12,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.则 该圆锥的底面半径为
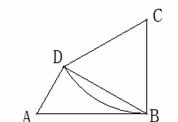
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com