
求证:等腰三角形底边上任意一点到两腰的距离之和等于定值.
|
已知:如图所示,在△ ABC中,AB=AC,P为BC上任意一点,PD⊥AB,PE⊥AC,垂足分别为D,E.求证:PD+PE是定值.
证法1:如图所示,
连接AP,过点B作BF⊥AC,垂足为F. ∵ 又∵ ∴ ∵AB=AC,∴PD+PE=BF,即PD+PE为定值. 证法2:如图所示,过点B作BF⊥AC,垂足为F,过点P作PG⊥BF,垂足为G.
∵ BF⊥AC,PE⊥AC,PG⊥BF,∴∠ FGP=∠GFE=∠PEF=90°,∴四边形 PEFG是矩形.∴ PE=GF,PG∥EF.∴∠ GPB=∠C.∵ AB=AC,∴∠ABC=∠C, ∴∠GPB=∠ABC. ∵PD⊥AB,PG⊥BF, ∴∠PDB=∠PGB=90°. 在△BDP和△PGB中,
∴△ BDP≌△PGB,∴GB=PD, ∴PD+PE=BF. 证法3:如图所示,过点C作CF⊥AB,垂足为F,过点C作GC⊥PD,交DP的延长线于G.
∵ GC⊥DP,PD⊥AB,CF⊥AB,∴∠ G=∠CFD=∠GDF=90°.∴四边形 CGDF是矩形,∴ CG∥AB,GD=CF,∴∠ PCG=∠B.∵ AB=AC,∴∠B=∠ACB, ∴∠PCG=∠ACB. ∵PE⊥AC, ∴∠PEC=90°. ∴∠PEC=∠G. 在△PEC和△PGC中,
∴△ PEC≌△PGC,∴PE=PG. ∴PD+PE=PG+PD=CF,即PD+PE为定值. |
|
这种题首先要探求出这个定值,由于 P是底边BC上一个动点,那么它的极端位置当然是在端点上了,不妨设点P运动到B点,此时PD=0,PE为腰AC上的高(高是不变量),那么只需证明PD+PE等于一腰上的高就可以了. |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
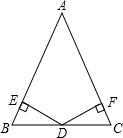 求证:等腰三角形底边上的中点到两腰的距离相等.结合所给图形,把“已知”、“求证”补充完整,并完成证明过程.
求证:等腰三角形底边上的中点到两腰的距离相等.结合所给图形,把“已知”、“求证”补充完整,并完成证明过程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com