
��֪������ABCD�У�MΪBC����һ�㣬 AB=BM=10��MC=14����ͼ1��������EFGH�Ķ���E�͵�B�غϣ���F��G��H�ֱ��ڱ�AB��AM��BC��.��ͼ2��PΪ�Խ���AC��һ���㣬������EFGH��ͼ1��λ�ó�������ÿ��1����λ���ٶ���BC���C�����ƶ���ͬʱ����P��C���������ÿ��1����λ���ٶ���CA���A�����ƶ�.����F�����߶�AC��ʱ��������EFGH�͵�Pͬʱֹͣ�˶�.���˶�ʱ��Ϊt�룬����������⣺
��1���������˶������У�����F�����߶�AM�Ϻ͵�G�����߶�AC��ʱ���ֱ������Ӧt��ֵ��
��2���������˶������У���������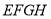 ��
��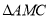 �ص��������ΪS,��ֱ��д��S��t֮��ĺ�����ϵʽ�Լ��Ա���t��ȡֵ��Χ��
�ص��������ΪS,��ֱ��д��S��t֮��ĺ�����ϵʽ�Լ��Ա���t��ȡֵ��Χ��
��3���������˶������У��Ƿ���ڵ�P,ʹ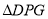 ����DGΪ���ĵ��������Σ������ڣ����t��ֵ���������ڣ�˵������.
����DGΪ���ĵ��������Σ������ڣ����t��ֵ���������ڣ�˵������.

(1)5��7����2���𰸼���������3��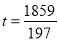 .
.
��������
�����������1�����������ε���λ������t��ֵ��
��2����5��λ�ù�ϵ�ֱ����ۣ�
��3�����Խ����Ե�BΪԭ���ֱ������ϵ����ʾ�������������������ľ��룬���������ľ��빫ʽ��ʾ�����ߵij��ȣ�Ȼ����������������ɹ���t������������⼴�ɡ�
���������(1)��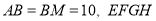 ������
������
��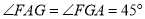
��
��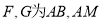 ���е�
���е�
��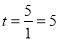 ��
��
�֡ߵ�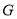 ����
����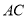 ��ʱ,����·��Ϊ
��ʱ,����·��Ϊ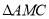 ����λ�ߵij�.
����λ�ߵij�.
�֡�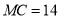
��
��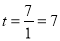 ��
��
(2)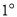 ��
��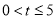 ʱ��
ʱ�� 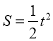
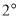 ��
��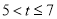 ʱ��
ʱ�� 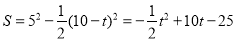
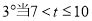 ʱ��
ʱ�� 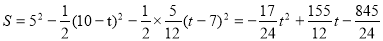
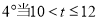 ʱ��
ʱ�� 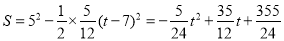

(3)��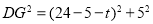
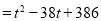
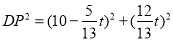
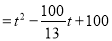
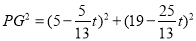
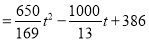

�ٵ�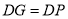 ʱ,
ʱ,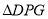 Ϊ����������
����������
��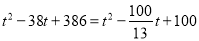 ��
��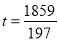 ��
��
�� ����ڵ�
����ڵ�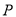 ,ʹ
,ʹ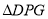 Ϊ����������
����������
�ڵ�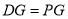 ʱ��
ʱ��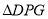 Ϊ����������
����������
��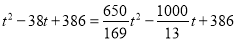
��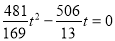 ��
��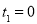 ����ȥ����
����ȥ���� 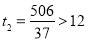 ����ȥ��
����ȥ��
���ϣ����ڵ�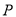 ,��
,��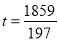 ��ʱ��
��ʱ��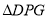 ����DGΪ���ĵ���������.
����DGΪ���ĵ���������.
������1.�����ε���λ�ߣ�2.���κ�����3.���������ε�����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2013-2014ѧ���������������ҿڸ���ѧУ���꼶��ѧ��������������ѧ�Ծ��������棩 ���ͣ������
��ͼ�� ABCD�Ķ���A��B������ֱ���A(-1��0)B��0��-2��������C��D��˫����
ABCD�Ķ���A��B������ֱ���A(-1��0)B��0��-2��������C��D��˫���� �ϣ���AD��y���ڵ�E����
�ϣ���AD��y���ڵ�E���� ABCD���������ABE�����8������k= ��
ABCD���������ABE�����8������k= ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ���������������ҿڸ���ѧУ���꼶��ѧ�������������ѧ�Ծ��������棩 ���ͣ�ѡ����
���������У���ȷ���ǣ��� ��.
A�� B��
B��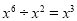 C��
C��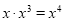 D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ���������������ҿڸ���ѧУ���꼶��ѧ��������������ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ��������y=ax2+bx+c��x�ύ�ڵ�A����1��0������������Ϊ��1��n������y��Ľ����ڣ�0��2������0��3��֮�䣨�����˵㣩�������н��ۣ�����x��3ʱ��y��0����3a+b��0������1��a�ܩ�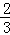 ����3��n��4�У���ȷ���ǣ���������
����3��n��4�У���ȷ���ǣ���������
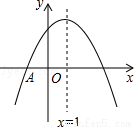
A���٢� B���ۢ� C���٢� D���٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ���������������ҿڸ���ѧУ���꼶��ѧ��������������ѧ�Ծ��������棩 ���ͣ�ѡ����
�ݱ����������о�������2013��GDP����ԼΪ770��Ԫ���ÿ�ѧ��������ʾ��һ����ӦΪ�� �� �� ��Ԫ��
A�� Ԫ B��
Ԫ B��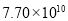 Ԫ C��
Ԫ C��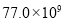 Ԫ D��
Ԫ D��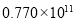 Ԫ
Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�������о��꼶3���¿���ѧ�Ծ��������棩 ���ͣ������
�Ȼ�������ֵ�� ������
������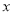 Ϊ����ʽ��
Ϊ����ʽ��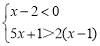 ��������.
��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�������о��꼶3���¿���ѧ�Ծ��������棩 ���ͣ������
������x�ķ��� 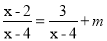 �⣬��m=________.
�⣬��m=________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�������о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����һ��ע�ض�ѧ�����ۺ�����������ÿ�ڶ�����չ�ḻ��ʵĿ�����3����Ѯ��������ӣ�����£���һ�����꼶�����ˡ�������һ��������������������ʫ�����лᣬ�꼶���༶�������룮ѧУΪ����ͬѧ�ǵĻ����ԣ��Բ���༶�����˽���������һ�����������ĵȼ��������ڸ��辫������ͬʱҲ����һ�������ʽ�����Ϊ�����ȼ�������һ����Ӧ�Ľ�Ʒ.���ݻ������ij����ͬѧ���Ƴ�����������������ͳ��ͼ���ĸ��ȼ������Ľ�Ʒ�۸��ñ����ʾ.
�ȼ� | �۸�Ԫ/���� |
һ�� | 100 |
���� | 60 |
���� | 40 |
�ĵ� | 20 |

��1�����꼶���� ���༶�μӴ˴λ�����л�ö��Ƚ��İ༶�� �����벹ȫ����ͳ��ͼ��
��2��������ͳ��ͼ�У����Ƚ��������ε�Բ�ĽǵĶ����� �ȣ���Щ��Ʒ��ƽ���۸��� Ԫ��
��3���ڴ˴λ�У����һ�Ƚ��İ༶���������༶���Գ�һ�꼶����ö��Ƚ��İ༶��Ҳֻ�������༶���Գ�һ�꼶��ѧУ���ӻ��һ�����Ƚ��İ༶�и�ѡ��һ���༶����ѧУ�μ����������������û���״ͼ���б���ķ��������ѡ�༶����ͬһ�꼶�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ������ʡ�̽����п���һ��ģ�⿼����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ���ڡ�ABC�У�AC=BC����D��E�ֱ��DZ�AB��AC���е㣬����ADE�Ƶ�E��ת180��á�CFE�����ı���ADCFһ���ǣ���

A������ B������ C�������� D������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com