
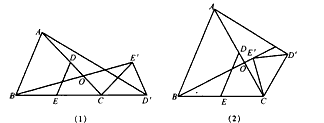
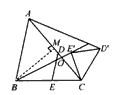
| 解:(1)1; (2)∵DE∥AB, ∴ △CDE∽△CAB, ∴ 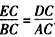 由旋转图形的性质得,EC=E′C,DC=D′C, ∴  ∵∠ECD=∠E′CD′, ∴∠ECD+∠ACE′=∠ E′CD′+∠ACE′,即∠BCE′=∠ACD′ ∴△BCE′∽△ACD′ ∴  ; ;(3)作BM⊥AC于点M,则BM=BC·sin60°, ∵为BC中点, ∴CE= 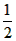 BC=2, BC=2,△CDE旋转时,点E′在以点C为圆心、CE长为半径的圆上运动 ∵CO随着∠CBE′的增大而增大, ∴当BE′与⊙C相切时,即∠BE′C=90°时最大,则CO最大, ∴此时∠CBE′=30°,CE′= 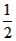 BC=2=CE BC=2=CE∴点E′在AC上,即点E′与点O重合, ∴CO=CE′=2, 又∵CO最大时,AO最小,且AO=AC-CO=3, ∴S△OAB最小= 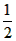 AO · BM=3 AO · BM=3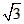 。 。 |
 |


科目:初中数学 来源: 题型:
 已知:△ABC中,AB=AC.
已知:△ABC中,AB=AC.查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-相似的判定解答题(带解析) 题型:解答题
如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm.动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停止运动,以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
(1)当t= _________ s时,点P与点Q重合;
(2)当t= _________ s时,点D在QF上;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-相似的判定解答题(解析版) 题型:解答题
如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm.动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停止运动,以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
(1)当t= _________ s时,点P与点Q重合;
(2)当t= _________ s时,点D在QF上;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com