
(本题满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角 (
( 且
且 ≠ 90°),得到Rt△
≠ 90°),得到Rt△ ,
,
(1)如图9,当 边经过点B时,求旋转角
边经过点B时,求旋转角 的度数;
的度数;
(2)在三角板旋转的过程中,边 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 交
交 边于点E,联结BE.
边于点E,联结BE.
①当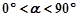 时,设
时,设 ,
, ,求
,求 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域;
②当 时,求
时,求 的长.
的长.


解:(1)在Rt△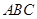 中,∵∠A=30°,
中,∵∠A=30°,
∴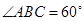 .………………………………………………………(1分)
.………………………………………………………(1分)
由旋转可知: ,
, ,
,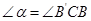
∴△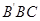 为等边三角形.……………(2分)
为等边三角形.……………(2分)
∴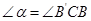 =
=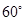 .……………(1分)
.……………(1分)
(2)①
当 时,点D在AB边上(如图).
时,点D在AB边上(如图).

∵
DE∥ ,
,
∴  ..…………………………………………………(1分)
..…………………………………………………(1分)
由旋转性质可知,CA =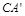 ,CB=
,CB=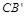 ,
∠ACD=∠BCE.
,
∠ACD=∠BCE.
∴  ,.…………………………………………………(1分)
,.…………………………………………………(1分)
∴ 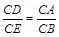 .
.
∴ △CAD∽△CBE. .………………………………………(1分)
∴ .
.
∵∠A=30°
∴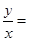
 .……………………………………………(1分)
.……………………………………………(1分)
∴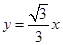 (0﹤
(0﹤ ﹤2)…………………………………………(2分)
﹤2)…………………………………………(2分)
②当 时,点D在AB边上
时,点D在AB边上
AD=x,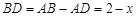 ,∠DBE=90°.
,∠DBE=90°.
此时, .
.
当S
= 时,
时,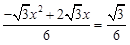 .
.
整理,得 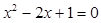 .
.
解得  ,即AD=1. …………………………………(2分)
,即AD=1. …………………………………(2分)
当 时,点D在AB的延长线上(如图)
时,点D在AB的延长线上(如图)
 .
.
仍设AD=x,则 ,∠DBE=90°..
,∠DBE=90°..
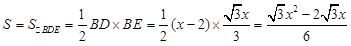 .
.
当S
= 时,
时, .
.
整理,得  .
.
解得  ,
, (负值,舍去).
(负值,舍去).
即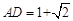 .…………………………………………………(2分)
.…………………………………………………(2分)
综上所述:AD=1或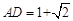 .
.
【解析】略


科目:初中数学 来源: 题型:
(本题满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角![]() (
(![]() 且
且![]() ≠ 90°),得到Rt△
≠ 90°),得到Rt△![]() ,
,
(1)如图9,当![]() 边经过点B时,求旋转角
边经过点B时,求旋转角![]() 的度数;
的度数;
(2)在三角板旋转的过程中,边![]() 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 交
交![]() 边于点E,联结BE.
边于点E,联结BE.
①当![]() 时,设
时,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数解析式及定义域;
之间的函数解析式及定义域;
②当![]() 时,求
时,求![]() 的长.
的长.


查看答案和解析>>
科目:初中数学 来源:2011届上海市普陀区4月中考模拟数学试卷 题型:解答题
(本题 满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角 (
( 且
且 ≠ 90°),得到Rt△
≠ 90°),得到Rt△ ,
,
(1)如图9,当 边经过点B时,求旋转角
边经过点B时,求旋转角 的度数;
的度数;
(2)在三角板旋转的过程中,边 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 交
交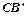 边于点E,联结BE.
边于点E,联结BE.
①当 时,设
时,设 ,
,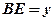 ,求
,求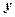 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域;
②当 时,求
时,求 的长.
的长. 

查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(天津卷)数学 题型:解答题
(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN, .
.
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A、C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出函数的定义域;
(3)若△AME∽△ENB(△AME的顶点A、M 、E分别与△ENB的顶点E、N、B对应),求AP的
、E分别与△ENB的顶点E、N、B对应),求AP的 长.
长.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(天津卷)数学 题型:解答题
(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN, .
.
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A、C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出函数的定义域;
(3)若△AME∽△ENB(△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应),求AP的长.

查看答案和解析>>
科目:初中数学 来源:2010-2011学年上海市考模拟数学试卷 题型:解答题
(本题满分14分,第(1)、(2)小题每小题满分5分,第(3)小题满分4分)
已知,在边长为6的正方形ABCD的两侧如图作正方形BEFG、正方形DMNK,恰好使得N、A、F三点在一直线上,联结MF交线段AD于点P,联结NP,设正方形BEFG的边长为x,正方形DMNK的边长为y,
(1)求y关于x的函数关系式及自变量x的取值范围;
(2)当△NPF的面积为32时,求x的值;
(3)以P为圆心,AP为半径的圆能否与以G为圆心,GF为半径的圆相切,若能请求x的值,若不能,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com