
分析 先根据a+$\frac{1}{a}$=m,得a2+1=ma,再整体代入即可得出答案.
解答 解:∵a+$\frac{1}{a}$=m,
∴a2+1=ma,
∴$\frac{{a}^{4}+1}{{a}^{2}}$=$\frac{(ma-1)^{2}+1}{ma-1}$
=$\frac{m{a}^{2}-2ma+2}{ma-1}$
=$\frac{m(ma-1)-2ma+2}{ma-1}$
=$\frac{{m}^{2}a-m-2ma+2}{ma-1}$
=$\frac{m(ma-1)-2(ma-1)}{ma-1}$
=m-2.
故答案为m-2.
点评 本题考查了分式的混合运算,把分式化到最简,再整体代入是解答的关键.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:填空题
| t/s | 1 | 2 | 3 | 4 | … |
| s/m | 6 | 8 | 10 | 12 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲驾车从A地去往B地,到达后停留3个小时,然后返回,往返车速都为120千米/时,乙驾车从B地去往A地,到达后停留1.5小时,因事提前返回,乙往返的车速不变,如图是两车距A地的路程s(千米0与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:
甲驾车从A地去往B地,到达后停留3个小时,然后返回,往返车速都为120千米/时,乙驾车从B地去往A地,到达后停留1.5小时,因事提前返回,乙往返的车速不变,如图是两车距A地的路程s(千米0与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知两条直线l1、l2分别经过点A(-1,0)、点B(3,0)并且当两条直线同时相交于y轴的负半轴上的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l1交于点K,与直线l2交于点E,在x轴交于点F,D是抛物线的顶点,如图所示.
已知两条直线l1、l2分别经过点A(-1,0)、点B(3,0)并且当两条直线同时相交于y轴的负半轴上的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l1交于点K,与直线l2交于点E,在x轴交于点F,D是抛物线的顶点,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
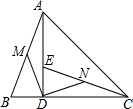 如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.
如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com