方程x2-y2=2010的整数解的组数为12．题目和参考答案——青夏教育精英家教网—

7．方程x²-y²=2010的整数解的组数为12．

分析由平方差公式可知x²-y²=（x+y）（x-y），（x+y）与（x-y）是奇数或者偶数，将2010分为两个数的积，分别解方程组即可．

解答解：∵2010=1×2010=（-1）×（-2010）=10×201=（-10）×（-201）=（2）×（1005）=（-2）×（-1005），
∴（x+y），（x-y）分别可取下列数对
（1，2010），（2010，1），（-1，-2010），（-2010，-1），
（10，201），（201，10），（-10，-201），（-201，-10），
（2，1005）、（-2，-1005）、（1005，2）、（-1005，-2），
由此可得方程有12组整数解．
故答案为12

点评本题主要考查非一次不定方程的知识点，解答本题的关键是掌握平方差公式的实际运用，应明确两整数之和与两整数之积的奇偶性相同．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

17．

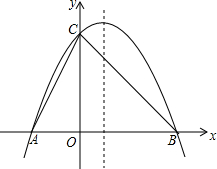如图，已知抛物线y=ax²-2ax+4与x轴交于A、B两点，与y轴交于点C，且OB=OC．
（1）求抛物线的函数表达式；
（2）若过A、B、C三点作一个外接圆，请求出这个圆的圆心M的坐标；
（3）在坐标平面内点P到A、B、C三点的距离分别为d₁、d₂、d₃，若d₁=2d₂=d₃，请求出点P的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

18．2π是一个（　　）

A．

整数

B．

分数

C．

偶数

D．

无理数

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

15．

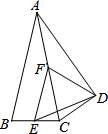如图，△ABC中，AB=AC，以AC为斜边作Rt△ADC，使∠ADC=90°，∠CAD=∠CAB=26°，E、F分别是BC、AC的中点，则∠EDF等于51°．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．问题1：在图1中，已知线段AB，CD，它们的中点分别为E，F．
①若A（-2，0），B（4，0），则E点坐标为（1，0）；
②若C（-1，3），D（-1，-2），则F点坐标为（-1，$\frac{1}{2}$）；
问题2：在图2中，无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A（a，b），B（c，d），AB中点为D（x，y）时，请直接写出D点的坐标（$\frac{a+c}{2}$，$\frac{b+d}{2}$）；（用含a、b、c、d的式子表示）．
问题3：如图3，一次函数y=x-4与反比例函数y=$\frac{5}{x}$的图象交于A、B两点，若以A、O、B、P为顶点的四边形是平行四边形，请直接写出顶点P的坐标（4，-4）或（6，6）或（-6，-6）．