48
分析:在等腰△OAC和△OCD中,根据等腰三角形的两个底角相等的性质求得∠OCD=∠ODC、∠CAO=∠OCA,所以由三角形的内角和求得∠OCD=48°;然后根据角平分线的性质求得∴∠OCA=∠ACD=24°;最后由圆周角定理知:∠ABD=

∠AOD,∠OCA=

∠AOD.所以∠ABD=∠CAO,进而求得∠ABD+∠CAO=48°.
解答:∵圆心角的度数和它们对的弧的度数相等,
∴

的度数等于84°,即∠COD=84°;
在△COD中,OC=OD(⊙O的半径),
∴∠OCD=∠ODC(等边对等角);
又∵∠COD+∠OCD+∠ODC=180°,
∴∠OCD=48°;
而CA是∠OCD的平分线,
∴∠OCA=∠ACD,
∴∠OCA=∠ACD=24°;
在△AOC中,OA=OC(⊙O的半径),
∴∠CAO=∠OCA(等边对等角);
∵∠ABD=

∠AOD(同弧所对的圆周角是所对的圆心角的一半),
∠DCA=

∠AOD(同弧所对的圆周角是所对的圆心角的一半),
∴∠ABD=∠CAD,
∴∠ABD+∠CAO=48°;
故答案为:48°.
点评:本题综合考查了圆周角定理和圆心角、弧、弦的关系.解答此题的关键点是利用“圆心角的度数和它们对的弧的度数相等”求得∠COD=84°.

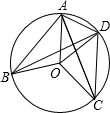 如图,点A,B,C,D都在⊙O上,
如图,点A,B,C,D都在⊙O上, 的度数等于84°,CA是∠OCD的平分线,则∠ABD+∠CAO=________°.
的度数等于84°,CA是∠OCD的平分线,则∠ABD+∠CAO=________°. ∠AOD,∠OCA=
∠AOD,∠OCA= ∠AOD.所以∠ABD=∠CAO,进而求得∠ABD+∠CAO=48°.
∠AOD.所以∠ABD=∠CAO,进而求得∠ABD+∠CAO=48°. 的度数等于84°,即∠COD=84°;
的度数等于84°,即∠COD=84°; ∠AOD(同弧所对的圆周角是所对的圆心角的一半),
∠AOD(同弧所对的圆周角是所对的圆心角的一半), ∠AOD(同弧所对的圆周角是所对的圆心角的一半),
∠AOD(同弧所对的圆周角是所对的圆心角的一半),

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°. 如图,点A的坐标为(2
如图,点A的坐标为(2