
如图,已知在扇形OAB中,∠AOB=90°,半径OA=10,正方形FCDE的四个顶点分别在 和半径OA、OB上,则CD的长为
.
和半径OA、OB上,则CD的长为
.

2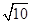 .
.
【解析】
试题分析:过点O作OH⊥CF于点H,交DE于点K,连接OF,由垂径定理可知CH=HF,因为四边形FCDE是正方形故OH⊥DE,DK=EK,所以△OEK是等腰直角三角形,OK=EK,设CD=x,则HK=x,HF=OK=EK=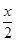 ,在Rt△OGF中根据勾股定理可得出x的值,进而得出结论.
,在Rt△OGF中根据勾股定理可得出x的值,进而得出结论.
试题解析:过点O作OH⊥CF于点H,交DE于点K,连接OF,如图:
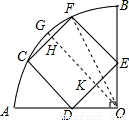
∵OH过圆心,
∴CH=HF,
∵四边形FCDE是正方形,
∴OH⊥DE,DK=EK,
∴△OEK是等腰直角三角形,OK=EK,
设CD=x,则HK=x,HF=OK=EK=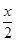 ,
,
在Rt△OGF中,OH2+HF2=OF2,即(x+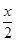 )2+(
)2+(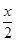 )2=102,解得x=2
)2=102,解得x=2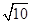 .
.
即CD的长为2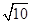 .
.
故答案为:2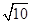 .
.
考点: 1.垂径定理;2.勾股定理;3.正方形的性质.


科目:初中数学 来源: 题型:
| 15 |
| 2 |
| A、3πcm | ||
| B、4πcm | ||
C、
| ||
| D、5πcm |
查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| AB |
| 1 |
| 3 |
 |
| AB |
| 19 |
| 3 |
| 5 |

查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
已知圆心角都是90°的扇形OAB与扇形OCD,如图所示那样叠放在一起,连接AC,BD.
(1)求证△AOC≌△BOD;

(2)若OA=3cm,OC=1cm,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:2010年福建省龙岩市一中对新罗区录取保送生加试数学试卷(解析版) 题型:选择题
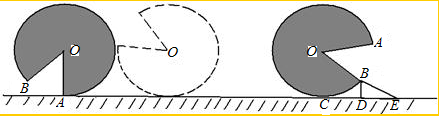
 的扇形AOB,半径OA=3cm,且OA与地面垂直.在没有滑动的情况下,将扇形向右滚动至与三角块BDE接触为止,此时,扇形与地面的接触点为C,已知∠BCD=30°,则O点移动的距离为( )
的扇形AOB,半径OA=3cm,且OA与地面垂直.在没有滑动的情况下,将扇形向右滚动至与三角块BDE接触为止,此时,扇形与地面的接触点为C,已知∠BCD=30°,则O点移动的距离为( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com