
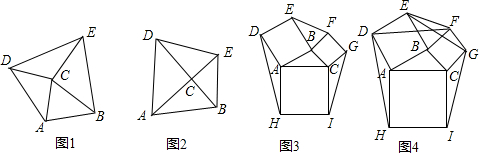
分析 (1)先证明∠DCE=90°,然后依据SAS证明△DCE≌△ACB,由全等三角形的性质可得到△ABC与△DCE的面积相等.
(2)过点A作AG⊥BC,过点D作DF⊥CE,垂足为F.先依据AAS证明△DCF≌△ACG,依据全等三角形的性质FD=AG,由等腰三角形的定义可知CE=CB,最后依据三角形的面积公式证明即可;
(3)①由(2)可知:S△ADH+S△BEF+S△CGI=3S△ABC,故此当∠ACB=90°,时S△ADH+S△BEF+S△CGI有最大值;②由①可知当∠ACB=90°,然后根据题意画出图形,接下来,证明点E、B、C在同一条直线上,从而可将△DEF的面积用含AB的式子表示,同理可将△EFG的面积用含BC的式子表示,最后在△ABC中,依据勾股定理进行解答即可.
解答 解:(1)如图1所示: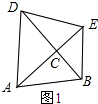
∵△ACD和△BCE均为等腰直角三角形,
∴DC=AC,CE=CB,∠ACD=∠BCE=90°.
∵∠ACB=∠ACD=∠BCE=90°,
∴∠DCE=90°.
在△DEC和△ABC中,$\left\{\begin{array}{l}{DC=AC}\\{∠ACB=∠DCE}\\{CE=CB}\end{array}\right.$,
∴△DCE≌△ACB.
∴△ABC与△DCE的面积相等.
(2)成立.
理由:如图2所示:过点A作AG⊥BC,过点D作DF⊥CE,垂足为F.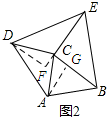
∵△ACD和△BCE均为等腰直角三角形,
∴∠DCA=∠ECB=∠FCB=90°,DC=AC,CE=CB.
∵FE⊥BC,AG⊥CB,
∴FC∥AG.
∴∠FCA=∠GAC.
∵∠DCF+∠FCA=90°,∠FCA+∠ACG=90°,
∴∠DCF=∠ACG.
在△DCF和△ACG中,$\left\{\begin{array}{l}{∠DFC=∠CGA}\\{∠DCF=∠ACG}\\{DC=AC}\end{array}\right.$,
∴△DCF≌△ACG.
∴FD=AG.
又∵CE=CB.
∴$\frac{1}{2}$CE•DC=$\frac{1}{2}$CB•AG,即△ABC与△DCE的面积相等.
(3)①如图3所示: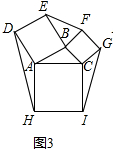
∵由(2)可知:S△ADH=S△ABC、S△BEF=S△ABC、S△CGI=S△ABC,
∴S△ADH+S△BEF+S△CGI=3S△ABC.
∴当∠ACB=90°,时S△ADH+S△BEF+S△CGI有最大值,最大值=3×$\frac{1}{2}$×3×4=18.
故答案为:∠ACB=90°;18.
②S△DEF+S△EFG=$\frac{1}{2}$S正方形AHIC.
理由:由①可知当∠ABC=90°时,S△ADH+S△BEF+S△CGI有最大值.
当∠ACB=90°时,如图4所示: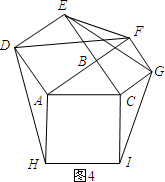
∵四边形ABED为正方形,
∴∠ABE=90°.
又∵∠ABC=90°,
∴∠ABE+∠ABC=90°+90°=180°.
∴点E、B、C在一条直线上.
∴△DEF的面积=$\frac{1}{2}$ED•AD=$\frac{1}{2}$AB2.
同理:△EFG的面积=$\frac{1}{2}$FG•CG=$\frac{1}{2}$CB2.
∵AC2=AB2+BC2,
∴S△DEF+S△EFG=$\frac{1}{2}$AB2+$\frac{1}{2}$CB2=$\frac{1}{2}$AC2=$\frac{1}{2}$S正方形AHIC.
∴S△DEF+S△EFG=$\frac{1}{2}$S正方形AHIC.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了等腰直角三角形的性质、正方形的性质、全等三角形的性质和判定、三角形的面积公式、勾股定理的应用,掌握本题的辅助线的作法是解答本题(2)的关键;明确当∠ACB=90°,时S△ADH+S△BEF+S△CGI有最大值是解答问题(3)的关键.


科目:初中数学 来源: 题型:解答题

| 类别 | 篮球 | 足球 | 排球 |
| 进价(单位:元/个) | 50 | 30 | 20 |
| 预售价(单位:元/个) | 70 | 45 | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
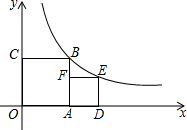 如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )| A. | $({\frac{{\sqrt{5}-1}}{2},\frac{{\sqrt{5}+1}}{2}})$ | B. | $({\frac{{\sqrt{5}+1}}{2},\frac{{\sqrt{5}-1}}{2}})$ | C. | $({\frac{{\sqrt{5}}}{2},-\frac{{\sqrt{5}}}{2}})$ | D. | (1,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2018的坐标是(-505,505).
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2018的坐标是(-505,505).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )| A. | 2$\sqrt{3}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
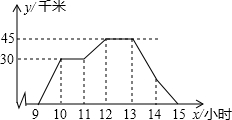 A、B两地路程为45千米,图中折线表示骑车人离A地的路程y与时间x的函数关系,一辆客车10:30从A地出发,沿与骑车人相同的路线以45千米/时的速度往返于A、B两地之间(往返中不停留),以下结论正确的个数有( )
A、B两地路程为45千米,图中折线表示骑车人离A地的路程y与时间x的函数关系,一辆客车10:30从A地出发,沿与骑车人相同的路线以45千米/时的速度往返于A、B两地之间(往返中不停留),以下结论正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com