
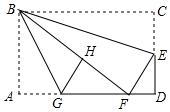
 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:分析 利用折叠性质得∠CBE=∠FBE,∠ABG=∠FBG,BF=BC=10,BH=BA=6,AG=GH,则可得到∠EBG=$\frac{1}{2}$∠ABC,于是可对①进行判断;在Rt△ABF中利用勾股定理计算出AF=8,则DF=AD-AF=2,设AG=x,则GH=x,GF=8-x,HF=BF-BH=4,利用勾股定理得到x2+42=(8-x)2,解得x=3,所以AG=3,GF=5,于是可对②进行判断;接着证明△ABF∽△DFE,利用相似比得到$\frac{DE}{DF}$=$\frac{AF}{AB}$=$\frac{4}{3}$,而$\frac{AB}{AG}$=$\frac{6}{3}$=2,所以$\frac{AB}{AG}$≠$\frac{DE}{DF}$,所以△DEF与△ABG不相似,于是可对③进行判断;分别计算S△ABG和S△GHF可对④进行判断.
解答 解:∵△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,
∴∠CBE=∠FBE,∠ABG=∠FBG,BF=BC=10,BH=BA=6,AG=GH,
∴∠EBG=∠EBF+∠FBG=$\frac{1}{2}$∠CBF+$\frac{1}{2}$∠ABF=$\frac{1}{2}$∠ABC=45°,所以①正确;
在Rt△ABF中,AF=$\sqrt{B{F}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴DF=AD-AF=10-8=2,
设AG=x,则GH=x,GF=8-x,HF=BF-BH=10-6=4,
在Rt△GFH中,∵GH2+HF2=GF2,
∴x2+42=(8-x)2,解得x=3,
∴GF=5,
∴AG+DF=FG=5,所以②正确;
∵△BCE沿BE折叠,点C恰落在边AD上的点F处
∴∠BFE=∠C=90°,
∴∠EFD+∠AFB=90°,
而∠AFB+∠ABF=90°,
∴∠ABF=∠EFD,
∴△ABF∽△DFE,
∴$\frac{AB}{DF}$=$\frac{AF}{DE}$,
∴$\frac{DE}{DF}$=$\frac{AF}{AB}$=$\frac{8}{6}$=$\frac{4}{3}$,
而$\frac{AB}{AG}$=$\frac{6}{3}$=2,
∴$\frac{AB}{AG}$≠$\frac{DE}{DF}$,
∴△DEF与△ABG不相似;所以③错误.
∵S△ABG=$\frac{1}{2}$×6×3=9,S△GHF=$\frac{1}{2}$×3×4=6,
∴S△ABG=1.5S△FGH.所以④正确.
故答案为①②④.
点评 本题考查了三角形相似的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用;在利用相似三角形的性质时,主要利用相似比计算线段的长.也考查了折叠和矩形的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>-2 | B. | m>2 | C. | m<-2 | D. | m<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,AD是中线,BC=10,∠B=∠DAC,则线段AC的长为( )
如图,△ABC中,AD是中线,BC=10,∠B=∠DAC,则线段AC的长为( )| A. | 4 | B. | 5 | C. | 5$\sqrt{2}$ | D. | 5$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
如图,一次函数y=kx+b的图象分别与反比例函数y=$\frac{a}{x}$的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
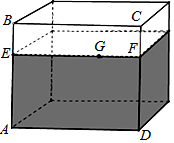 有一个如图所示的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE=40cm,在水面上紧贴内壁G处有一块面包屑,G在水面线EF上,且EG=60cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬进鱼缸内的G处面包屑.
有一个如图所示的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE=40cm,在水面上紧贴内壁G处有一块面包屑,G在水面线EF上,且EG=60cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬进鱼缸内的G处面包屑.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com