
如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是
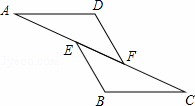
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
|
分析∶求出AF=CE,再根据全等三角形的判定定理判断即可. 解答∶解∶∵AE=CF, ∴AE+EF=CF+EF, ∴AF=CE, A、∵在△ADF和△CBE中 ∴△ADF≌△CBE(ASA),正确,故本选项错误; B、根据AD=CB,AF=CE,∠AFD=∠CEB不能推出△ADF≌△CBE,错误,故本选项正确; C、∵在△ADF和△CBE中 ∴△ADF≌△CBE(SAS),正确,故本选项错误; D、∵AD∥BC, ∴∠A=∠C, ∵在△ADF和△CBE中 ∴△ADF≌△CBE(ASA),正确,故本选项错误; 故选B 点评∶本题考查了平行线性质,全等三角形的判定的应用,注意∶全等三角形的判定定理有SAS,ASA,AAS,SSS. |
|
考点∶全等三角形的判定. |


科目:初中数学 来源:2008年湖北省天门市初中毕业升学统一考试、数学试卷 题型:022
如图,已知AE=CF,∠A=∠C,要使△ADF≌△CBE,还需添加一个条件________(只需写一个).
查看答案和解析>>
科目:初中数学 来源:2012-2013学年云南红河弥勒西二中学八年级下学期期末测试数学试卷(带解析) 题型:解答题
如图,在□ABCD中,E、F分别在边BA、DC的延长线上,已知AE=CF,P、Q分别是DE和FB的中点,求证:四边形EQFP是平行四边形.
查看答案和解析>>
科目:初中数学 来源:2014届云南红河弥勒西二中学八年级下学期期末测试数学试卷(解析版) 题型:解答题
如图,在□ABCD中,E、F分别在边BA、DC的延长线上,已知AE=CF,P、Q分别是DE和FB的中点,求证:四边形EQFP是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com